Question

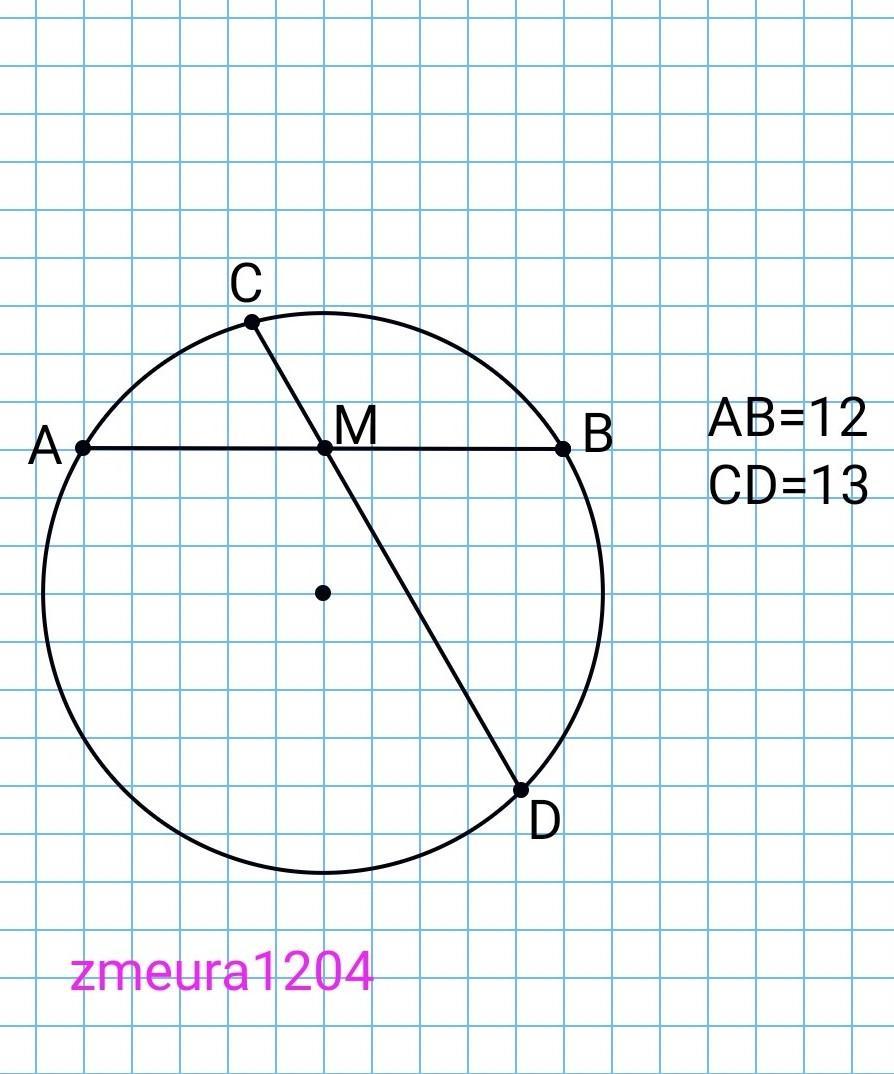
AB and CD are chords in a circle. Chord CD passes through the
midpoint M of the chord AB. Given that AB = 12, CD = 13,
and CM < DM. Find CM.

Answer 1

Ответ:

CM=4

Объяснение:

AM=MB, M- midpoint of the chord AB.

АМ=АВ/2=12/2=6

АМ=МВ=6

CM=x; MD=(13-x)

Intersecting chords theorem:

If two chords intersect in the circle, then the products of the measures of the segment of the chords are iqual:

CM*MD=AM*MB

х(13-х)=6*6

13х-х²=36

13х-х²-36=0. |×(-1)

х²-13х+36=0

х=(-b±√(b²-4ac))/2a;

x=(13±√(13²-4*36))/2=

=(13±√(169-144))/2=(13±√25)/2;

x1=(13+5)/2=18/2=9

x2=(13-5)/2=8/2=4

CM<DM; 4<9

CM=4; DM=9