пожалуйста,решите задание
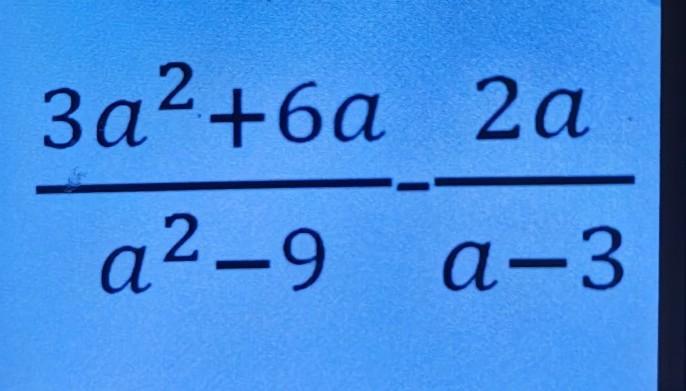
Ответы
Ответ:
Давайте рассмотрим каждое уравнение по отдельности.
1. 3a² + 6a - 2a:
В этом уравнении присутствует квадратичный терм (a²) и два линейных терма (6a и -2a).
Чтобы решить это уравнение, мы можем сначала объединить мономы с одинаковыми степенями переменной a:
3a² + 6a - 2a = 3a² + 4a
Полученное уравнение уже упрощено и не может быть решено, так как у нас есть только одно слагаемое с переменной a.
2. a² - 9a - 3:
В этом уравнении также присутствуют квадратичный терм (a²) и два линейных терма (-9a и -3).
Для решения можно использовать различные методы, включая факторизацию, завершение квадрата или формулу квадратного корня.
Давайте попытаемся факторизовать это уравнение. Для начала, посмотрим на коэффициент при квадратичном терме (a²), который равен 1. Затем, посмотрим на свободное слагаемое (-3), чтобы узнать его разложение на множители.
Разложение -3 на множители может быть, например, -1 3 или 1 -3.
Теперь давайте подумаем о комбинациях множителей, которые могут дать нам коэффициент при линейном слагаемом (-9a). Возможными комбинациями являются:
1 -3 = -3 и -1 3 = -3
Коэффициент при a равен -9, поэтому пробуем комбинацию -1 * 3, чтобы разложить это уравнение на множители:
(a + 1)(a - 3)
Таким образом, исходное уравнение a² - 9a - 3 можно факторизовать следующим образом:
(a + 1)(a - 3) = 0
Теперь мы можем применить свойство нулевого произведения, которое гласит, что если произведение равно нулю, то хотя бы один из множителей должен быть равен нулю:
a + 1 = 0 или a - 3 = 0
Отсюда мы получаем два возможных решения:
a = -1 или a = 3
Мы рассмотрели оба заданных уравнения и получили их решения. Если у вас есть дополнительные вопросы или вы хотите узнать о других способах решения уравнений, не стесняйтесь задавать!