У чотирикутнику ABCD сторони BC і AD паралельні. Чи може бути що кут A=103°, кут B=27°, кут C=77°, кут D=153°
Ответы
НЕ МОЖЕТ
1) Сумма углов четырёхугольника равна 360°
∠A + ∠B + ∠C + ∠D = 103 +27 +77 +153 = 360°
следовательно ABCD четырёхугольник
2) Но по условию задачи BC || AD
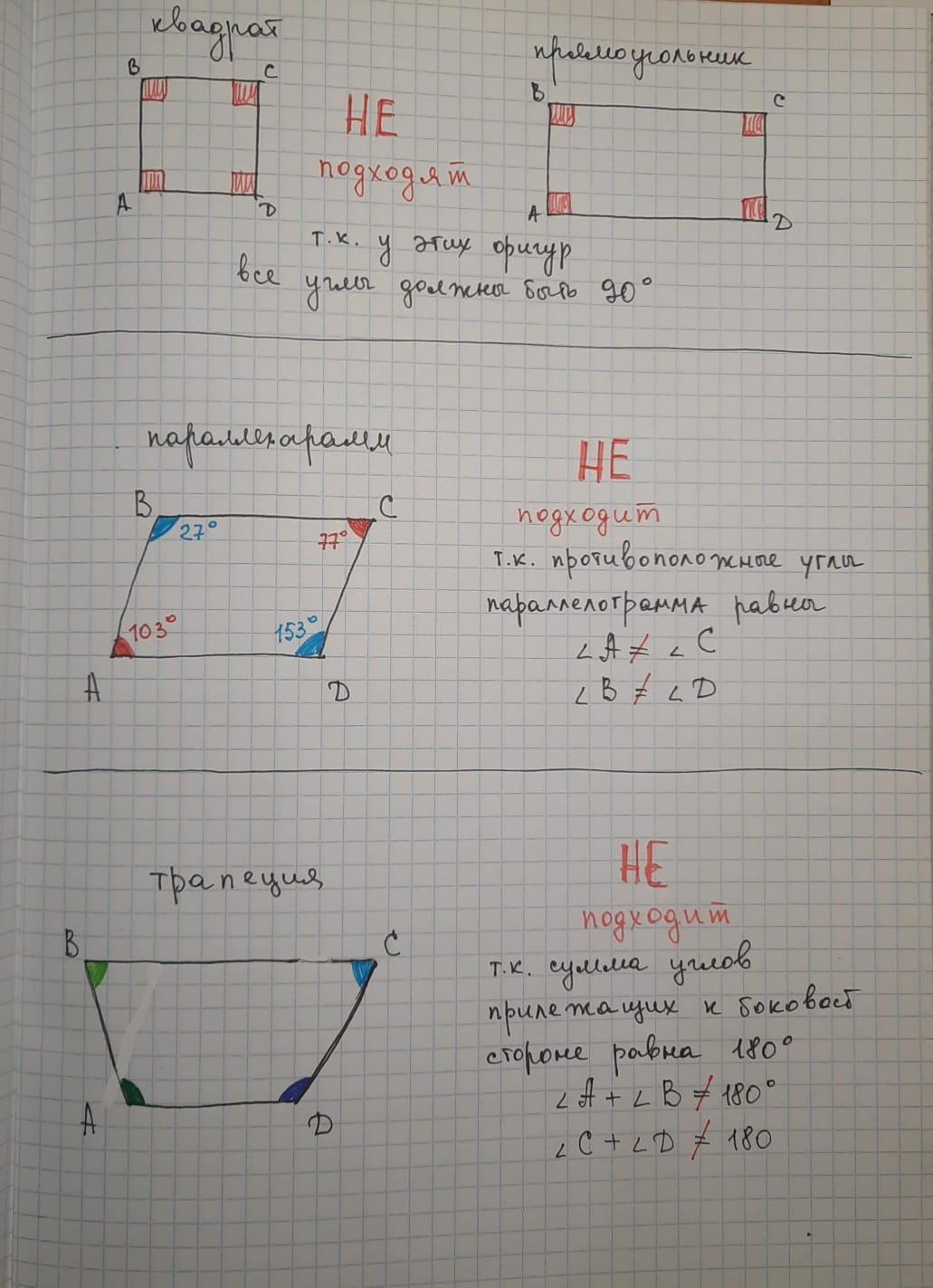
Рассмотрим четырёхугольники с противоположно параллельными сторонами: квадрат
прямоугольник
параллелограмм
трапеция
Квадрат и прямоугольник НЕ подходят,
т.к. у этих квадрата и прямоугольника все углы по 90°,
а у нас по условию все углы разные.
Параллелограмм НЕ подходит,
т.к. по свойству параллелограмма противолежащие углы равны,
а у нас по условию ∠A ≠ ∠C и ∠B ≠ ∠D
Трапеция НЕ подходит, т.к. по свойству трапеции
углы, прилежащие к боковой стороне = 180°,
а у нас по условию ∠A + ∠B = 103 + 27 = 130 ≠ 180°
∠С + ∠D = 77 + 153 = 230 ≠ 180°
ВЫВОД:
четырехугольник ABCD
с параллельными сторонами BC || AD
НЕ МОЖЕТ ИМЕТЬ углы ∠А=103°, ∠ B=27°, ∠C=77°, ∠D=153°