Question

Вычислите площадь фигуры, ограниченной линиями:
1) у=х², у=0, х=4
2) у=-х²+х, у=0
3) у=соsx, y=0, x=0, x=п/6
Помогите пожалуйста
​

Answer 1

Ответ:

Объяснение:

Вычислите площадь фигуры, ограниченной линиями:

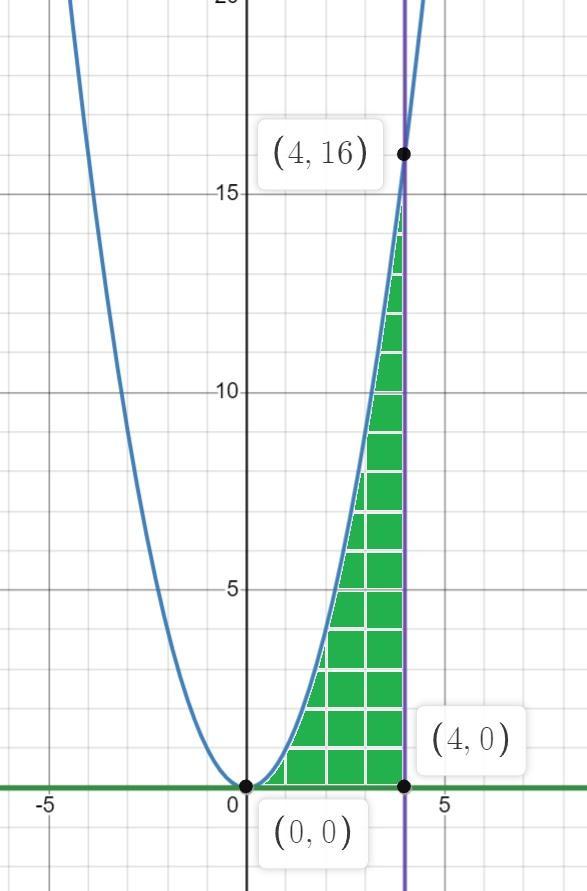
1) у=х²;  у=0;  х=4.

S=∫(a;b)f(x)dx

Пределы интегрирования   a=0;  b=4.  (См. скриншот)

f(x) = x².  Тогда

S=∫(0;4)x²dx = x³/3|(0;4) = 1/3(4³-0³) = 1/3*64 =  21 1/3 кв. ед.

****************************************

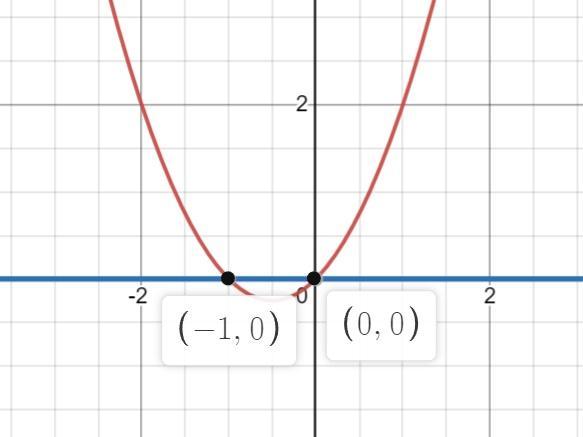
2) у=-х²+х;   у=0.

S=∫(a;b)f(x)dx;

Пределы интегрирования   a=-1;  b=0.  (См. скриншот)

f(x) = -х²+х.  Тогда

S=-∫(-1;0)(-x²+x)dx = -∫(-1;0)(-x²)dx - ∫(-1;0)xdx = -(-x³/3|(-1;0) - x²/2|(-1;0) =

= -(-1/3(0³-(-1)³) - 1/2(0²-(-1)²) = -(-1/3) - 1/2(-1) = 1/3+1/2 = 5/6 кв.ед.

**************************

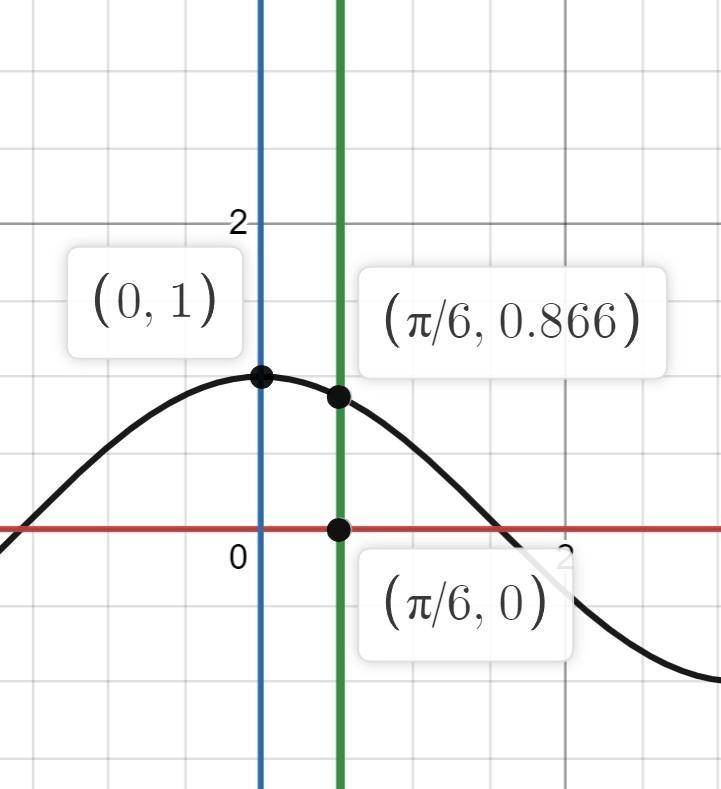
3) у=соs(x);  y=0;   x=0;   x=pi/6.

S=∫(a;b)f(x)dx.

Пределы интегрирования   a=0;  b=pi/6. (См. скриншот)

f(x) = cos(x).  Тогда

S = ∫(0;pi/6)cos(x)dx = sin(x)|(0;pi/6) = sin(pi/6) - sin(0) = 1/2-0 = 1/2 кв. ед.