Допоможіть будь ласка!!!
Розв’яжіть нерівність У відповідь запишіть кількість цілих розв’язків нерівності.
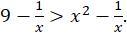
Ответы
Ответ:
4 целых решения неравенства.
Объяснение:
Приведем все члены уравнения к общему знаменателю х
Отсюда первое условие х ≠ 0 (условие 1)
Дальше. При равных знаменателях больше та дробь, у которой числитель больше.
Значит, мы получаем
9х - 1 > x³ -1
x³ -1 -9x + 1 < 0
x³ - 9x <0
Сначала решим уравнение x³ - 9x = 0
х(x² -9) = 0
х(х - 3)(х + 3) = 0
Произведение равно нулю, когда хотя бы один из сомножителей равен нулю.
Тогда у нас получается
х = 0 или х = 3 или х = (-3)
Но х не может быть равен 0 по условию 1.
Значит, остается два решения
х = 3 или х = (-3)
Дальше метод интервалов.
Наносим на числовую ось эти два значения и смотрим на каком интервале мы получим наше условие
(x² -9) < 0
это выполняется на интервале х ∈ (-3; 3)
Соединяем этот ответ с условием (1) и получаем решение нашего неравенства.
x ∈ (-3; 0) ∪ (0; 3)
И тогда целых решений будет
х = {-2; -1; 1; 2)
т.е 4 целых решения неравенства.