Предмет: Математика,
автор: asotfilipavic7
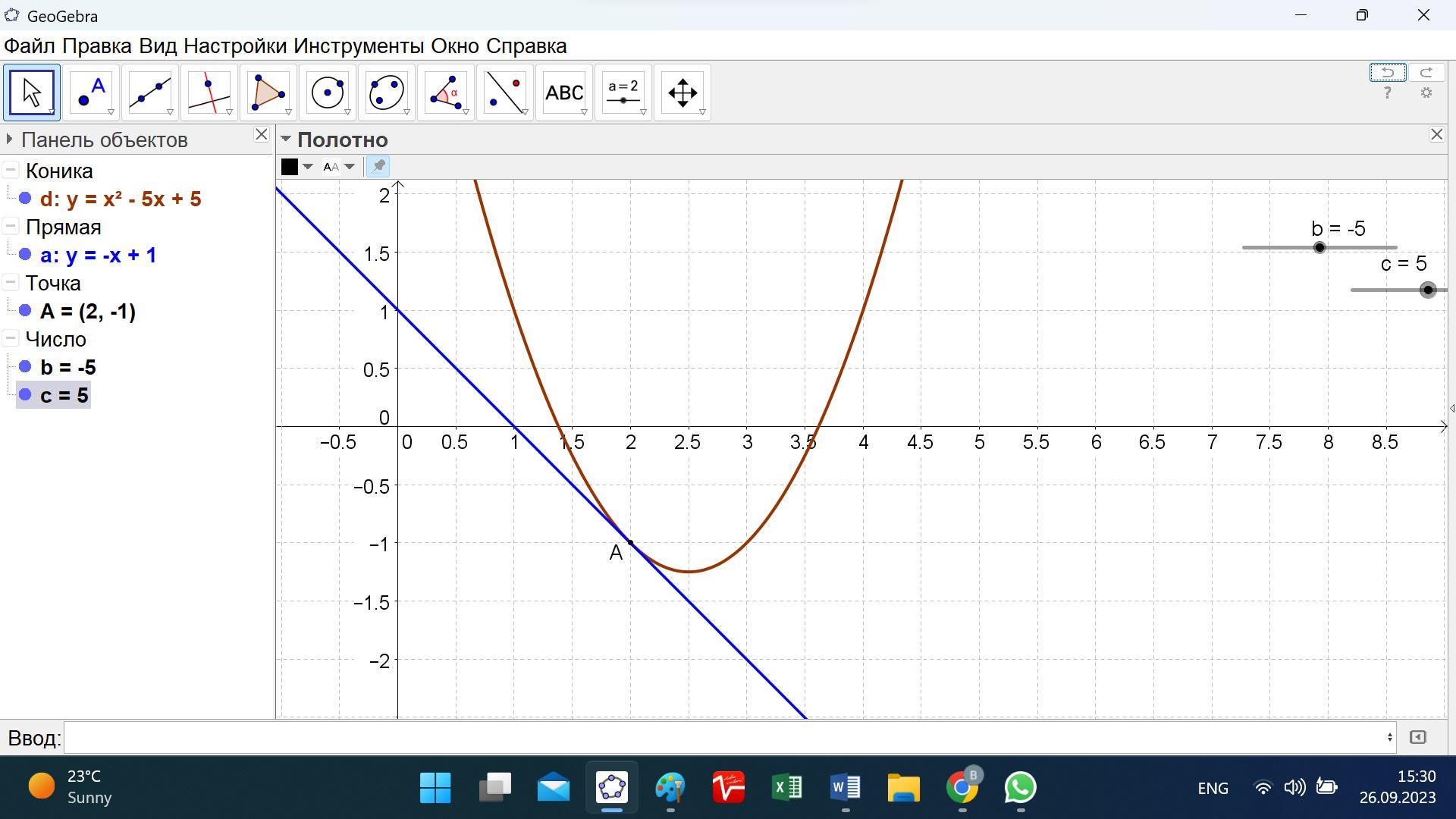
100 БАЛЛІВ!!! СРОЧНО!!! При яких значеннях b і c парабола y=x^2+bx+c дотикається до прямої y=−x+1 у точці з абсцисою x0=2
Приложения:

Ответы
Автор ответа:
1
Подставим х = 2 в уравнение прямой: у = -2 + 1 = -1.
Введём эти данные в уравнение параболы.
-1 = (-2)² + b*2 + c,
-1 = 4 + b*2 + c,
2b + c = -5.
Производная функции равна: y’ = 2x + b.
Уравнение касательной, проведенной к графику функции y=f(x) в точке x0, имеет вид: y=f(x0)+ f'(x0)(x-x0), где f(x0) - значение функции f(x) в точке х0, f'(x0) - значение производной данной функции в точке х0.
Так как производная равна угловому коэффициенту касательной, то приравняем: 2*2 + b = -1, отсюда находим значение b = -5.
Теперь, зная координаты точки А(2; -1), , подставим их в уравнение параболы.
-1 = 2² + (-5)*2 + с, отсюда с = -1 – 4 + 10 = 5.
Ответ: b = -5, с = 5.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: ponomarenkodenis2011
Предмет: Литература,
автор: aniapokrishka1602
Предмет: География,
автор: angelinasenuk24
Предмет: Биология,
автор: medinatynymgali