найти общий вид первоначальной для функции
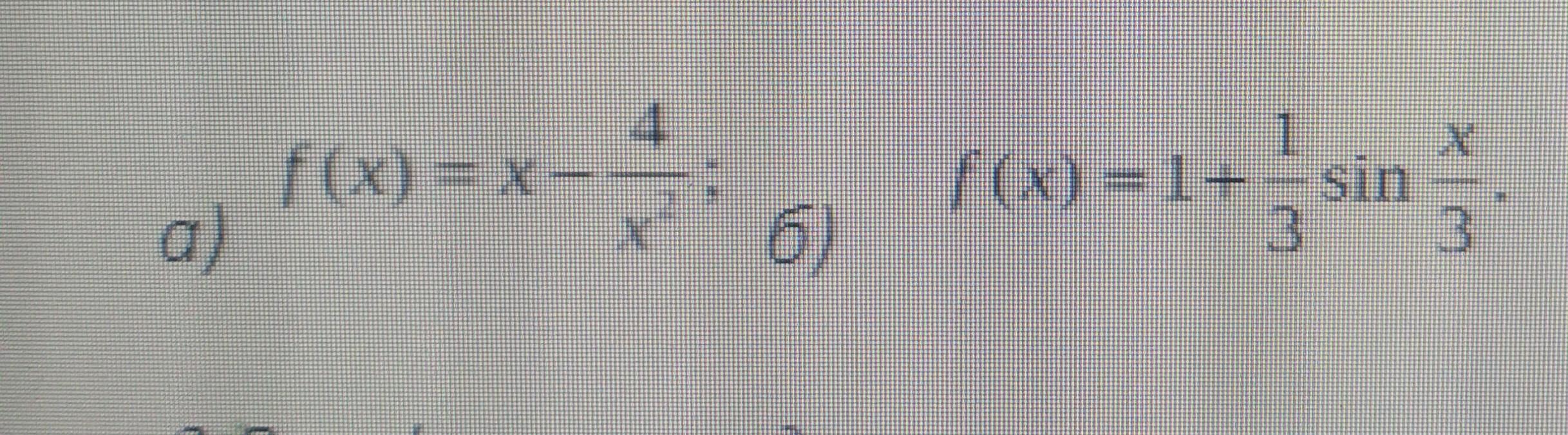
Ответы
Ответ:
Первая задача: f(x) = x - 4/x²
Это функция, которая имеет два корня: x = -2 и x = 2. Для того, чтобы найти эти корни, мы можем приравнять функцию к нулю и решить уравнение:
f(x) = x - 4/x² = 0
x² - 4 = 0
x² = 4
x = ±√4
x = ±2
Для того, чтобы изучить поведение функции, мы можем найти ее производную и точки экстремума. Производная функции f(x) равна:
f’(x) = 1 + 8/x³
Чтобы найти точки экстремума, мы приравниваем производную к нулю и решаем уравнение:
f’(x) = 1 + 8/x³ = 0
8/x³ = -1
x³ = -8
x = -2
Это единственная точка экстремума функции, и она является точкой минимума, так как f’'(-2) > 0. Значение функции в этой точке равно:
f(-2) = -2 - 4/(-2)² = -3
Вторая задача: f(x) = 1 +1/3 sin x/3
Это периодическая функция, которая колеблется между значениями 2/3 и 4/3 с периодом 6π. Для того, чтобы найти эти значения, мы можем использовать свойства синуса и знать, что он принимает максимальное значение 1 при x/3 = π/2 и минимальное значение -1 при x/3 = -π/2. Тогда:
f(x) = 1 +1/3 sin x/3
f(π/2) = 1 +1/3 sin π/6 = 4/3
f(-π/2) = 1 +1/3 sin -π/6 = 2/3
Для того, чтобы найти период функции, мы можем использовать формулу:
T = 2π/b,
где b - коэффициент при x в аргументе синуса. В нашем случае b = 1/3, поэтому:
T = 2π/(1/3) = 6π
Первая задача имеет два корня: x = -2 и x = 2. Вторая задача имеет максимальное значение 4/3 и минимальное значение 2/3.