Предмет: Математика,
автор: ilya01049
Довести нерівності:::::::::::
Приложения:
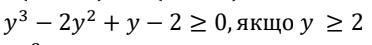
Ответы
Автор ответа:
0
Ответ:
Условие, которое вы представили, можно решить следующим образом:
Выразим уравнение y^3 - 2y^2 + y - 2 >= 0 как (y - 2)(y^2 + 1) >= 0.
Теперь мы видим, что это неравенство будет верным, если (y - 2) и (y^2 + 1) имеют одинаковые знаки.
1. Если y >= 2, то (y - 2) >= 0.
2. Выражение (y^2 + 1) всегда положительно, потому что квадрат любого числа (в данном случае, y) всегда неотрицательный, и прибавление 1 не изменяет знак.
Таким образом, оба множителя положительны, и их произведение также положительно. Так что неравенство y^3 - 2y^2 + y - 2 >= 0 верно, когда y >= 2.
Автор ответа:
0
Добуток невід’ємного числа на додатне число є додатним числом.
Похожие вопросы
Предмет: Українська мова,
автор: daniilmyzuchenko
Предмет: Химия,
автор: vladgoncar779
Предмет: Химия,
автор: ignatevaulia
Предмет: Математика,
автор: naatya889fil
Предмет: Биология,
автор: nastyarukavyshnykova