Предмет: Алгебра,
автор: kuanysabenov2
2.13. При каких значениях х имеет смысл выражение: 1) √3x; 2) √-3x; 4) √x-5; 5)√x + 9; 3) √x; 6) √7 - x ?
Приложения:
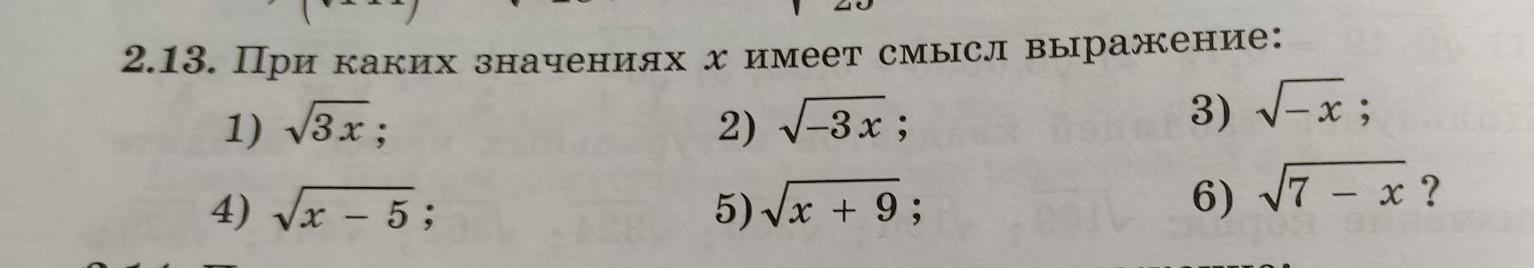
Ответы
Автор ответа:
1
Для того, щоб вираз мав сенс, під коренем необхідно мати невід'ємні значення аргументу. Записав відповідь у такій послідовності, оскільки задані лише номери задач і без порядку.
1) √3x: Вираз має сенс для будь-якого значення x.
2) √-3x: Вираз не має сенсу для будь-якого значення x, оскільки під коренем від'ємне число.
3) √x: Вираз має сенс для будь-якого невід'ємного значення x.
4) √x - 5: Вираз має сенс для будь-якого значення x, але зверніть увагу, що 5 має бути менше або дорівнювати кореню виразу x, щоб не отримати від'ємне значення під коренем.
5) √x + 9: Вираз має сенс для будь-якого невід'ємного значення x.
6) √7 - x: Вираз має сенс для будь-якого значення x, оскільки 7 має бути більше або дорівнювати x, щоб не отримати від'ємне значення під коренем.
Таким чином, для виразів 1), 3), 4), 5), і 6) можна підібрати значення x і вони матимуть сенс. Для виразу 2) не існує дійсних значень x, для яких вираз матиме сенс.
1) √3x: Вираз має сенс для будь-якого значення x.
2) √-3x: Вираз не має сенсу для будь-якого значення x, оскільки під коренем від'ємне число.
3) √x: Вираз має сенс для будь-якого невід'ємного значення x.
4) √x - 5: Вираз має сенс для будь-якого значення x, але зверніть увагу, що 5 має бути менше або дорівнювати кореню виразу x, щоб не отримати від'ємне значення під коренем.
5) √x + 9: Вираз має сенс для будь-якого невід'ємного значення x.
6) √7 - x: Вираз має сенс для будь-якого значення x, оскільки 7 має бути більше або дорівнювати x, щоб не отримати від'ємне значення під коренем.
Таким чином, для виразів 1), 3), 4), 5), і 6) можна підібрати значення x і вони матимуть сенс. Для виразу 2) не існує дійсних значень x, для яких вираз матиме сенс.
kokogaga901:
ахуеть
согл, я сам вахуй
Похожие вопросы
Предмет: Английский язык,
автор: baxodirovferuz9
Предмет: Английский язык,
автор: adiyagazizova
Предмет: Українська література,
автор: ladybugsupercat5
Предмет: Математика,
автор: salicromsali936
Предмет: Геометрия,
автор: mukanov0606