Question

В равнобедренном прямоугольном треугольнике длина каждой из медиан. проведённых к катетам, равна 5.Найти площадь треугольника.
Решите и объясните, пожалуйста!!!​

Answer 1

Ответ:

Объяснение:

Дано:
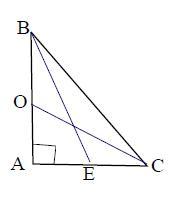
ΔВАС - равнобедренный
∠А = 90°
ВЕ, СО - медианы
ВЕ = СО = 5
-------------------
S(Δавс) = ?

1) Пусть АВ = х. Т.к. ΔВАС равнобедренный по условию, то
  АВ = АС = х
2) Т.к. ВЕ - медиана , а значит, делит сторону пополам, то
   АЕ =ЕС = х/2

3) Рассмотрим ΔВАЕ.
   ВЕ =5см по условию
   АВ = х
   АЕ = х/2
   ∠А = 90°
По т.Пифагора, квадрат гипотенузы  равен сумме квадратов катетов, т.е.
  АВ² + АЕ² = ВЕ² или

   х² +(х/2)² = 5²

   х² +(х²/4) = 25
  4х² + х² = 25*4
  5х² = 100
   х² = 100/5
   х² = 20, но  х = АВ= АС, тогда

АВ*АС = 20.
3) Площадь прямоугольного треугольника равна произведению его катетов, деленное на 2. Следовательно,
S(Δвас) = Ав*АС/2 = 20/2 = 10(кв.ед.)
Ответ: S(Δвас) = 10кв.ед.