Помогите пожалуйста решить, вероятность
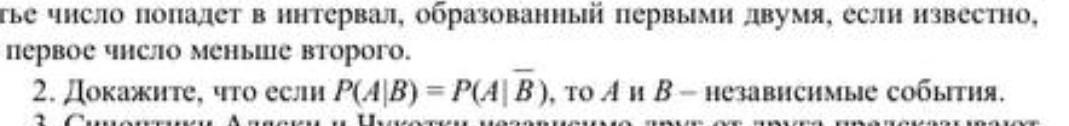
Ответы
Ответ:
Доказано требуемое.
Объяснение:
Исходя из житейского понимания независтимости событий, раз вероятность события A не зависит от того, произошло событие B или не произошло, значит события A и B независимы. Докажем, что житейское понимание независимости приводит к тому же ответу, что и математическое рассуждение.
Будем называть события A и B независимыми, если
P(AB)=P(A)·P(B).
Исходя из определения условной вероятности
мы можем заключить: при условии, что вероятность события B отлична от нуля, события A и B независимы, если P(A|B)=P(A).
Поскольку события и
образуют полную группу событий, мы можем воспользоваться формулой полной вероятности:
Вывод: события A и B независимы.