Решите только 4-ю задачу, учитывая что точка C лежит вне второй окружности

Ответы
Ответ:
Доказано требуемое.
Объяснение:
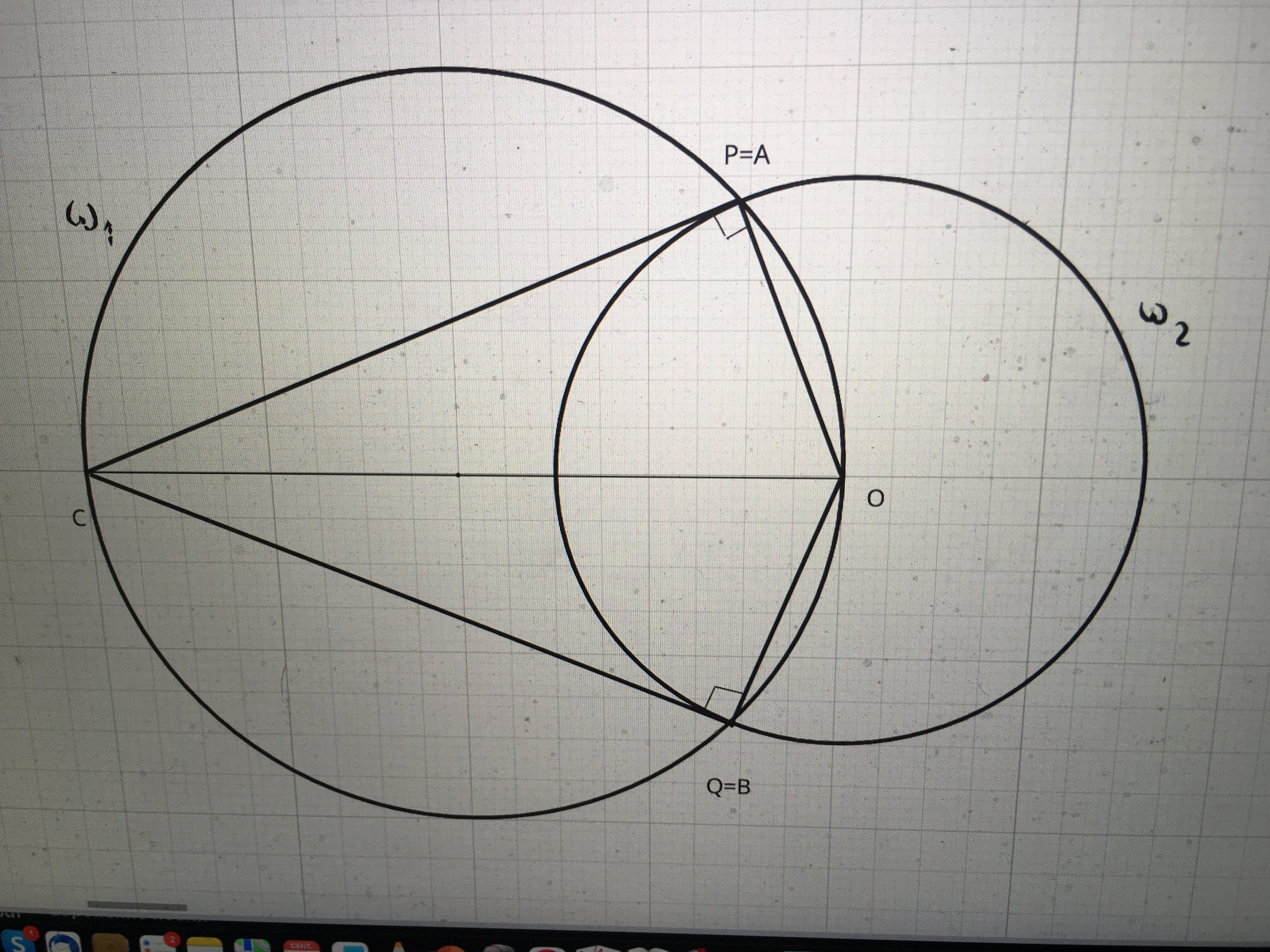
1-й случай. Точка C лежит на линии центров (см 1-й чертёж). В этом случае вписанные в первую окружность углы CPO и CQO опираются на диаметр и поэтому равны 90°, поэтому точки A и B совпадают с точками P и Q соответственно, откуда AB=PQ.
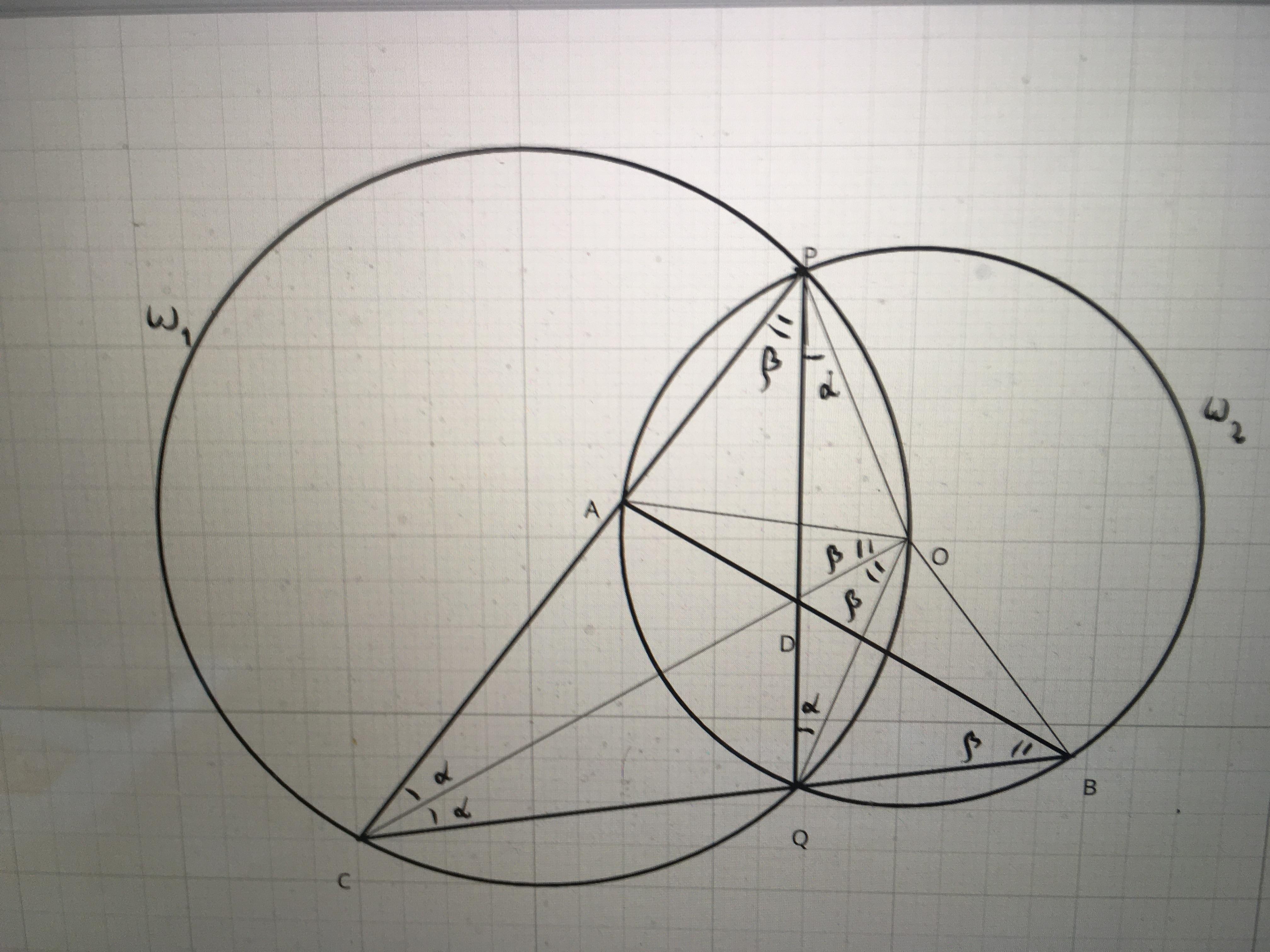
2-й случай. Точка C не лежит на линии центров; пусть для определённости она лежит ниже линии центров (см 2-й чертёж). Поскольку O - центр окружности, QO=AO.
Поскольку ∠AOQ - центральный, а ∠APQ вписанный, и они опираются нас одну дугу,
∠AOQ=2∠APQ=2∠CPQ=2∠COQ⇒∠AOC=∠COQ.
Поэтому треугольники CAO и CQO равны по двум сторонам и углу между ними ⇒ CA=CQ.
Далее, треугольники CPQ и CBA подобны (угол C общий, а углы P и B в этих треугольниках равны как вписанные во вторую окружность и опирающиеся на одну дугу), а поскольку CQ=CA, эти треугольники равны, и поэтому PQ=AB.