!!!СРОЧНО!!!ПОМОГИТЕ!!!!КАК РЕШИТЬ!!!!
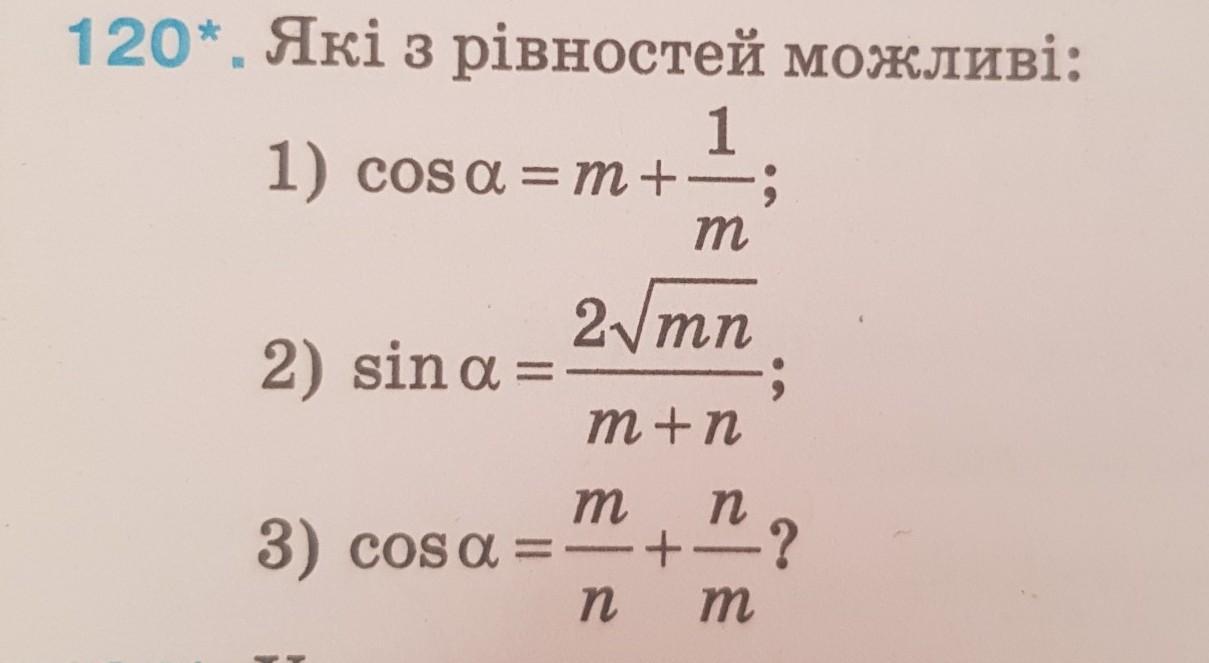
Ответы
Сінус і косінус не можуть бути меншими, ніж -1 і більшими, ніж 1.
І.
Треба визначити, чи є розв'язок у цієї системи нерівностей. Одразу відмітимо, що m ≠ 0.
Працюємо з першою нерівністю:
m² + 1 ≥ -m або m² + 1 ≤ -m
Mи так зробили тому що ми точно не знаємо знак m, на який ми помножили обі частини рівняння, тому два випадки.
- Перший:
m² + m + 1 ≥ 0, при m > 0
D = 1 - 4 = -3 (Вираз не дорівнює 0)
Цей вираз завжди більше 0, тому m ∈ R
- Другий:
m² + m + 1 ≤ 0, при m < 0
Ми вже з'ясували, що цей вираз завжди більше 0. Тому m ∈ ∅.
ітак, m ∈ (0; +∞)
Друга нерівність:
m² + 1 ≤ m або m² + 1 ≥ m
- Перший випадок:
m² - m + 1 ≤ 0, при m > 0
D = 1 - 4 = -3 (вираз не дорівнює 0)
Цей вираз теж завжди додатній. Тому m ∈ ∅
- Другий випадок:
m² - m + 1 ≥ 0, при m < 0
Так як вираз додатній, то m ∈ R.
ітак, m ∈ (-∞; 0)
Так як у нерівностей немає спільного проміжку, ми можемо сказати, що рівність
неможлива.
ІІ.
m + n ≠ 0.
У нас тут майже така нерівність:
середнє арифметичне ≥ середньому геометричному
щоб √mn існував, потрібно або щоб m і n були додатніми, або щоб m і n були від'ємними. Тому розглянемо два випадки:
- m i n додатні, або одне число додатнє, а друге 0.
тоді
додатнє число, а
від'ємне або 0. Тому що сам корінь завжди додатній або 0, а мінус робить від'ємним або залишає 0. Чи може бути додатнє менше від'ємного або 0? Ні. Тому нерівність не має розв'язків.
- m і n від'ємні або одне з них 0, а друге від'ємне.
Тоді ліва частина < 0, а права ≤ 0. Тоді нерівність завжди буде вірною, так як якщо ср.ариф ≥ ср.геом, тоді -ср.ариф ≤ ср.геом за властивістю нерівностей.
Друга нерівність:
Тут ми отримали ту саму нерівність ср.ариф ≥ ср.геом. І ми теж розглянемо два випадки.
- Перший випадок, m i n додатні або щось додатнє, а щось 0
В такому випадку нерівність завжди вірна.
- m i n від'ємні, або одне число від'ємне, а друге 0.
Тоді ліва частина від'ємна, а права додатня або 0. А додатне не може бути менше від'ємного та 0.
Що ми бачимо:
перша нерівність потребує, щоб одне число було < 0, а друге ≤ 0.
друга потребує, щоб одне число було > 0, а друге ≥ 0.
Оба числа не можуть бути 0. Також не може бути такого, що одне число додатнє, а друге від'ємне.
Спільного проміжку немає, тому рівність неможлива.
ІІІ.
n ≠ 0, m ≠ 0.
Перша нерівність:
І знов у нас декілька випадків.
- при m і n або >0, або <0.
Ця нерівність завжди вірна, так як додатнє завжди більше від'ємного.
- при m або n <0
Ця нерівність не вірна.
Друга нерівність:
- при m і n або >0, або <0.
Ця нерівність невірна.
- при m або n <0
Завжди виконується, так як mn від'ємне, а m² + n² додатнє.
Перша нерівність потребує або m i n з однаковими знаками, а друга з різними. m i n не можуть бути 0.
Рівність також не існує, так як немає спільних проміжків.