Предмет: Математика,
автор: salieri08
Решите пример с помощью математической индукции(см. фото).
Приложения:
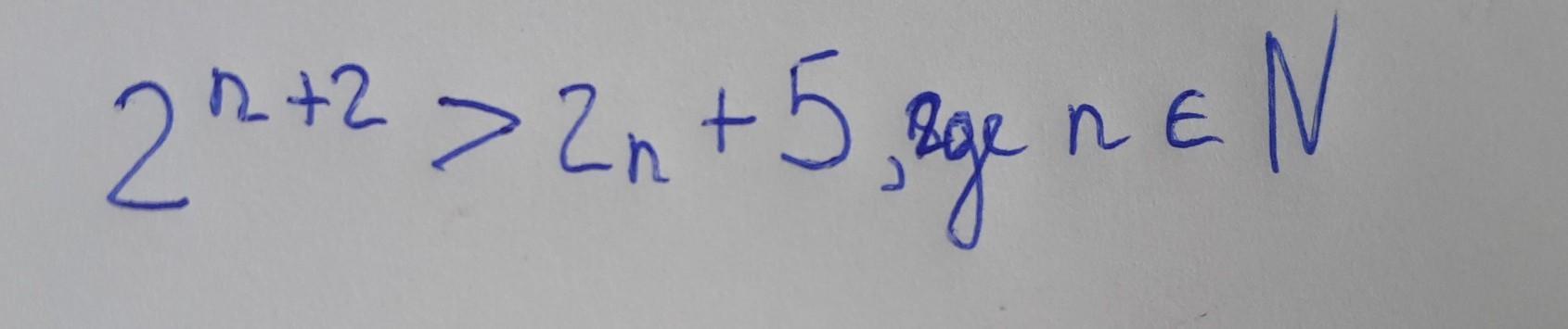
Ответы
Автор ответа:
1
1. Проверяем истинность утверждения для n = 1.
2. Предполагаем, что истинно для n = k (k - произвольное натуральное число).
3. Доказываем, что истинно, для n = k + 1.
Похожие вопросы
Предмет: Физика,
автор: dorotukalina5
Предмет: Литература,
автор: olegkush100
Предмет: Русский язык,
автор: albinanurdar
Предмет: Қазақ тiлi,
автор: molya0676
Предмет: Английский язык,
автор: zhanek2607