Question

1.Знайти площу паралелограма, коли відомо, що одна із сторін у 2,5 раза більша за другу, його периметр ДОРІВНЮЄ 28 см, а гострий кут 30градусів (зверніть увагу, що мова йде про паралелограм, а не прямокутник)

Answer 1

Ответ:

Площа паралелограму дорівнює 20 см²

Объяснение:

Знайти площу паралелограма, коли відомо, що одна із сторін у 2,5 раза більша за другу, його периметр ДОРІВНЮЄ 28 см, а гострий кут 30градусів.

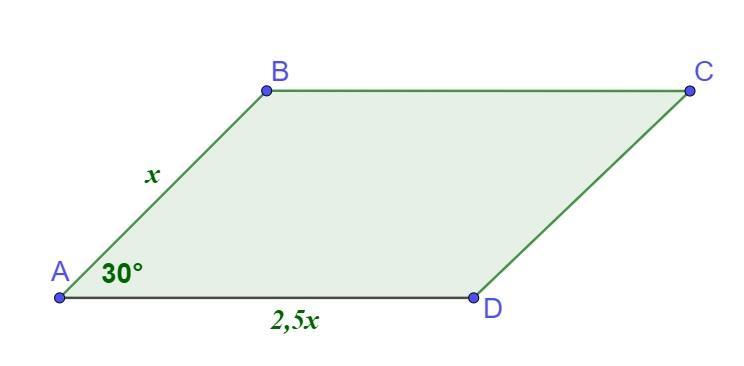
1) Нехай ABCD - даний паралелограм, тоді АВ = х см, а AD = 2,5х см (згідно умови). P(ABCD) = 28 см, ∠А = 30°.

Периметр паралелограма ABCD дорівнює подвоєній сумі довжин двох сусідніх сторін:

Р = 2(АВ + АD)

Складаємо рівняння:

2(х+2,5х)=28

3,5х=14

х=4

Отже, АВ = 4 см, AD = 2,5 · 4 = 10 см

2) Площа паралелограма дорівнює добутку довжин його сторін помноженому на синус кута між ними:

S = AB · AD · sin ∠A

S = 4 · 10 · sin 30° = 40 · 0,5 = 20 (см²)

ВІдповідь: 20 см²

#SPJ1