Question

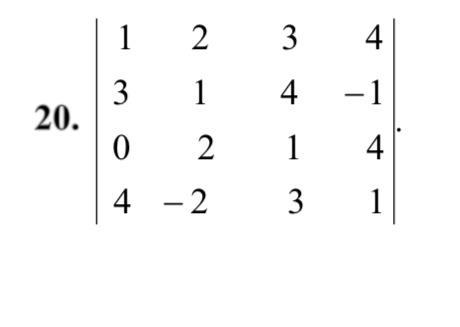
Вычислить определители четвертого порядка методом сведения к треугольному виду

Answer 1

Ответ:

$\left|\begin{array}{cccc}1&2&3&4\\3&1&4&-1\\0&2&1&4\\4&-2&3&1\end{array}\right|=49$

Решение:

$\left|\begin{array}{cccc}1&2&3&4\\3&1&4&-1\\0&2&1&4\\4&-2&3&1\end{array}\right|\ \boxed{=}$

От второй строки отнимем первую строку, умноженную на 3, а от четвертой строки отнимем первую строку, умноженную на 4:

$\boxed{=}\ \left|\begin{array}{cccc}1&2&3&4\\3-3\cdot1&1-3\cdot2&4-3\cdot3&-1-3\cdot4\\0&2&1&4\\4-4\cdot1&-2-4\cdot2&3-4\cdot3&1-4\cdot4\end{array}\right|=$

$=\left|\begin{array}{cccc}1&2&3&4\\0&-5&-5&-13\\0&2&1&4\\0&-10&-9&-15\end{array}\right|\ \boxed{=}$

Поменяем знаки во второй и четвертой строках определителя (при смене знака в двух строках определитель не меняется):

$\boxed{=}\ \left|\begin{array}{cccc}1&2&3&4\\0&5&5&13\\0&2&1&4\\0&10&9&15\end{array}\right|\ \boxed{=}$

Далее, чтобы не работать с дробными числами под знаком определителя, из второй строки вынесем за знак определителя множитель 1/2, тогда все числа во второй строке мы умножим на 2, а из третьей строки вынесем за знак определителя множитель 1/5, тогда все числа в третьей строке мы умножим на 5:

$\boxed{=}\ \dfrac{1}{2}\cdot\dfrac{1}{5}\cdot \left|\begin{array}{cccc}1&2&3&4\\0&10&10&26\\0&10&5&20\\0&10&9&15\end{array}\right|\ \boxed{=}$

Из третьей и из четвертой строки вычтем вторую строку:

$\boxed{=}\ \dfrac{1}{10}\cdot \left|\begin{array}{cccc}1&2&3&4\\0&10&10&26\\0&10-10&5-10&20-26\\0&10-10&9-10&15-26\end{array}\right|=\dfrac{1}{10}\cdot \left|\begin{array}{cccc}1&2&3&4\\0&10&10&26\\0&0&-5&-6\\0&0&-1&-11\end{array}\right|\ \boxed{=}$

Поменяем знаки в третьей и четвертой строках определителя:

$\boxed{=}\ \dfrac{1}{10}\cdot \left|\begin{array}{cccc}1&2&3&4\\0&10&10&26\\0&0&5&6\\0&0&1&11\end{array}\right|\ \boxed{=}$

Теперь поменяем местами третью и четвертую строки определителя, при этом знак определителя изменится на противоположный:

$\boxed{=}\ -\dfrac{1}{10}\cdot \left|\begin{array}{cccc}1&2&3&4\\0&10&10&26\\0&0&1&11 \\0&0&5&6\end{array}\right|\ \boxed{=}$

Наконец, из четвертой строки вычтем третью строку, умноженную на 5:

$\boxed{=}\ -\dfrac{1}{10}\cdot \left|\begin{array}{cccc}1&2&3&4\\0&10&10&26\\0&0&1&11 \\0&0&5-5\cdot1&6-5\cdot11\end{array}\right|=-\dfrac{1}{10}\cdot \left|\begin{array}{cccc}1&2&3&4\\0&10&10&26\\0&0&1&11 \\0&0&0&-49\end{array}\right|\ \boxed{=}$

Поскольку теперь определитель имеет треугольный вид, то его значение равно произведению элементов, стоящих на главной диагонали:

$\boxed{=}\ -\dfrac{1}{10} \cdot\Big(1\cdot10\cdot1\cdot(-49)\Big)=49$

Элементы теории:

Если определитель записан в треугольном виде, то есть все элементы, стоящие под главной диагональю, равны 0, то такой определитель равен произведению элементов, стоящих на главной диагонали:

$\left|\begin{array}{cccccc}a_{11}&a_{12}&a_{13}&\ldots&a_{1n} \\ 0&a_{22}&a_{23}&\ldots&a_{2n} \\0&0&a_{33}&\ldots&a_{3n} \\\ldots \\0&0&0&\ldots&a_{nn} \end{array}\right|=a_{11}a_{22}a_{33}\ldots a_{nn}=\prod\limits_{k=1}^n a_{kk}$

Основные свойства определителя:

1. Определитель не меняется:

• если к любой строке прибавить любые другие строки, умноженные на произвольные числа;
• при смене знаков в двух строках (или любом другом четном количестве строк).

2. Определитель меняет знак:

• при перестановке двух строк местами;
• при смене знаков в любой строке определителя. Однако, при смене знаков в двух строках определителя (предыдущий пункт) определитель не изменится (так как его знак сменился дважды, то есть фактически не изменился).

3. Общий множитель чисел строки можно вынести за знак определителя.