Предмет: Алгебра,
автор: erejzermilana
Пж ответ дам 50 балов
Приложения:

Ответы
Автор ответа:
1
Ответ:
Представить в виде степени и найти значение выражения .
Применяем свойства степеней (смотри вложение) .
Приложения:
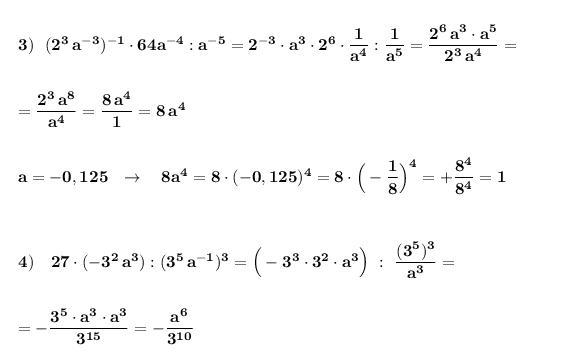
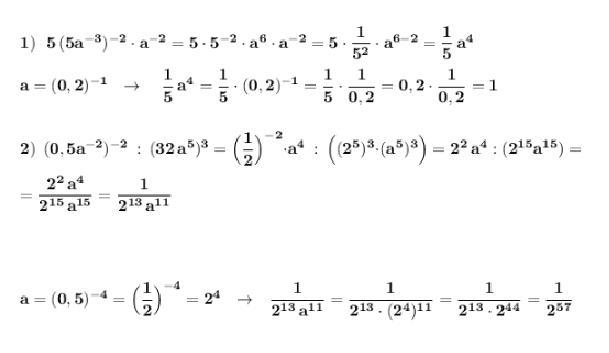

erejzermilana:
спасибо бро
I am sister
спасибо сестра
Похожие вопросы
Предмет: Химия,
автор: diasha201108
Предмет: Українська мова,
автор: mtlozynskyi
Предмет: Химия,
автор: dara83100
Предмет: Литература,
автор: infinityvit123
Предмет: Қазақ тiлi,
автор: dilnazegizbaeva7