Предмет: Алгебра,
автор: linarnugamanov
40 баллов !!!
Вычислите производную f'(x) при данном значении аргумента х
Приложения:
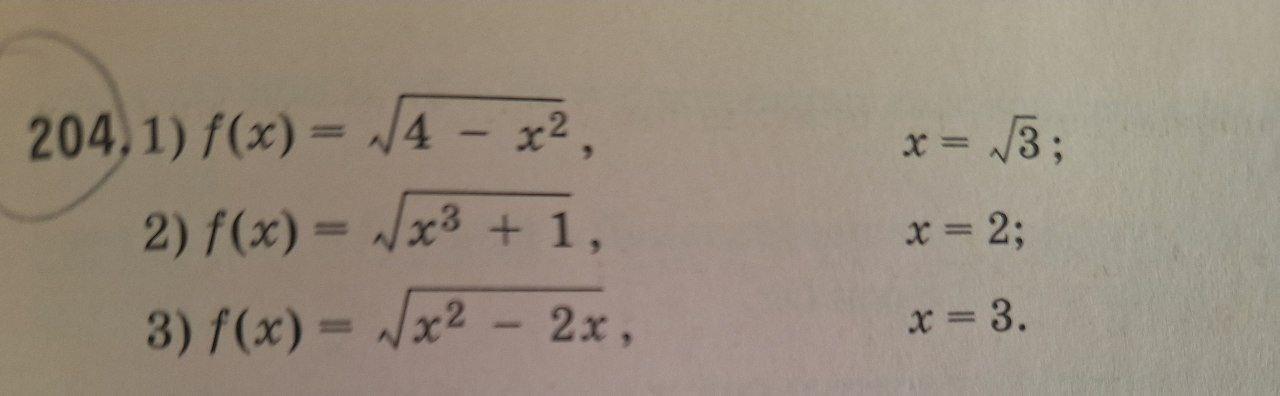
Ответы
Автор ответа:
1
Ответ:
Производная квадратного корня : , u - внутренняя
функция .
Приложения:

посмотрите этот вопрос
Похожие вопросы
Предмет: Русский язык,
автор: aidike771
Предмет: Литература,
автор: zhaniya1309z
Предмет: Математика,
автор: alexandrdovgani12
Предмет: Математика,
автор: yavoitov2017
Предмет: Математика,
автор: margotolstova310109
1.21 посчитать
1.31 сравнить числа
https://znanija.com/task/53413401?utm_source=android&utm_medium=share&utm_campaign=question