Обчислити площу плоскої фігури D, обмеженої зазначеними лініями:
Допоможіть рішить цей приклад буду дуже вдячний вам якщо ви зробите.))
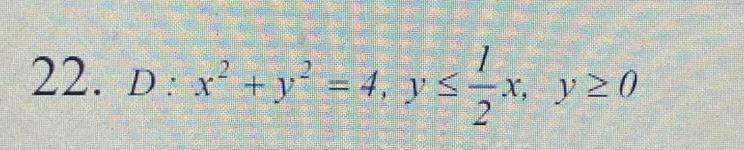
Ответы
Для обчислення площі плоскої фігури D, яка обмежена зазначеними лініями, спочатку треба знайти точки її перетину, а потім обчислити інтеграл відповідно до цих обмежень.
1. Знайдемо точки перетину ліній:
a) З лінією y = -x:
x² + y = 4
x² - x - 4 = 0
Застосуємо квадратне рівняння, щоб знайти значення x:
x = (-(-1) ± √((-1)² - 4*1*(-4))) / (2*1)
x = (1 ± √(1 + 16)) / 2
x₁ = (1 + √17) / 2
x₂ = (1 - √17) / 2
b) З лінією y = 0:
y = 0
2. Тепер ми знаємо точки перетину ліній:
x₁ = (1 + √17) / 2
x₂ = (1 - √17) / 2
3. Обчислимо інтеграл для обчислення площі фігури D:
Площа D = ∫[x₁, x₂] [4 - x²] dx
Площу можна обчислити таким чином:
Площа D = ∫[x₁, x₂] 4 dx - ∫[x₁, x₂] x² dx
4. Після обчислення цих інтегралів, ви отримаєте площу фігури D, яка обмежена зазначеними лініями.