Предмет: Алгебра,
автор: dosalymaryam
Памагите пажалуста срочна
Приложения:
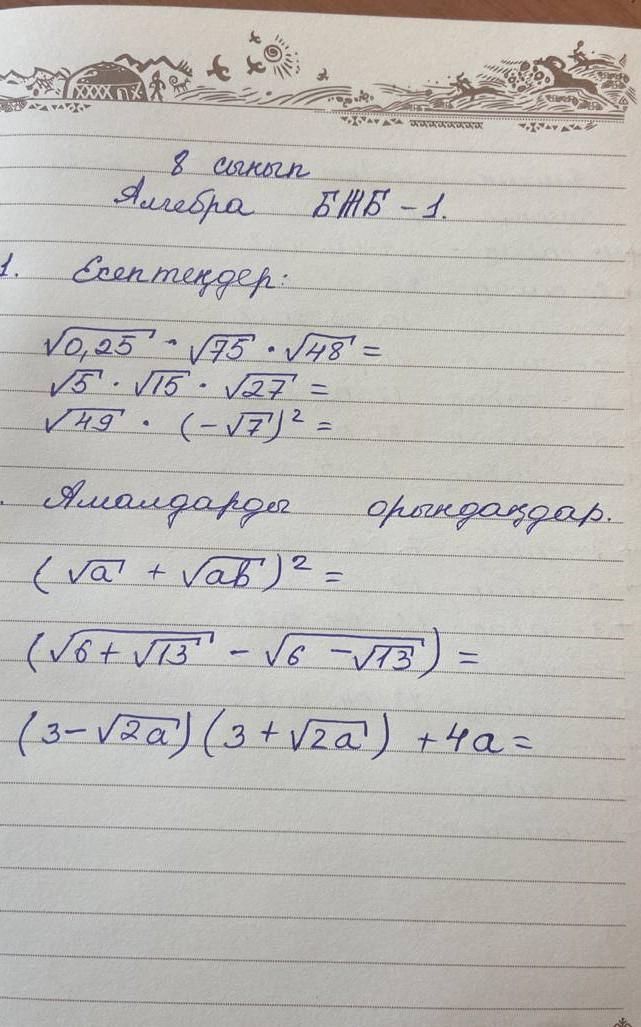
Ответы
Автор ответа:
1
Ответ:
Применяем свойствa корней : .
Применяем формулы квадрата суммы и разности , а также формулу разности
квадратов : ,
.
Приложения:


Похожие вопросы
Предмет: Математика,
автор: Nur356
Предмет: География,
автор: pavluko368
Предмет: Українська мова,
автор: viktotiahovrich
Предмет: Русский язык,
автор: felix0o
Предмет: Математика,
автор: komovaolga33