Предмет: Алгебра,
автор: weditakumi
Решите это уравнение развернуто. Буду очень благодарен
(4)/((x+1)^(2))+(2)/(1-x^(2))-(1)/(1-x)=0
Приложения:
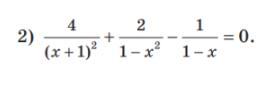
Ответы
Автор ответа:
0
(4)/((x+1)^(2)) + (2)/(1-x^(2)) - (1)/(1-x) = 0
Сначала умножим обе стороны уравнения на общий знаменатель, который равен (x+1)^(2)(1-x)(1-x).
4(1-x) + 2(x+1)^(2) - (1)(x+1)^(2)(1-x) = 0
Теперь раскроем скобки и упростим уравнение:
4 - 4x + 2(x^(2) + 2x + 1) - (x^(2) + 2x + 1)(1-x) = 0
Раскрываем скобки:
4 - 4x + 2x^(2) + 4x + 2 - x^(3) - 3x^(2) - x + 2 = 0
Сгруппируем по степеням x:
x^(3) - 3x^(2) + 2x^(2) - x + 4x - 4 + 2 = 0
x^(3) - x^(2) - x - 2 = 0
Теперь у нас есть кубическое уравнение. Его решение можно найти аналитически, используя методы алгебры или численные методы. Если вы хотите численное решение, то могу помочь с этим.
weditakumi:
Не брат, с ГПТ чата не прокатит, там ответ не точный и нет полного развернутого ответа и решения
ответил ведь,и помогло)
а так ты вопрос задал
лан
Похожие вопросы
Предмет: Английский язык,
автор: kuncicsofia2
Предмет: География,
автор: margaritatalan2
Предмет: Литература,
автор: nastyaleh1503
Предмет: Алгебра,
автор: ToshATube
Предмет: Математика,
автор: smartybook