Предмет: Алгебра,
автор: fix88
помогит пожалуйста знайти нулі функції
Приложения:
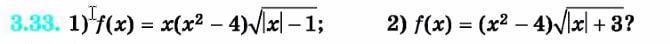
Ответы
Автор ответа:
0
Ответ:
1) x = {-2; -1; 1; 2}
2) х = {-2; 2}
Объяснение:
- произведение равно 0 если хотя бы один из сомножителей равен 0
1)
f(x) = 0 если х=0; или (х²-4)=0; или
Рассмотрим все случаи
х = 0.
(х²-4)=0 ⇒ х₁ = 2; х₂ = (-2)
⇒ х₁ = 1; х₂ = (-1)
Теперь обратим внимание на условие
Подкоренное выражение должно быть ≥ 0.
Отсюда следует что |x|-1 ≥ 0 при х≥1 или х ≤ (-1)
И тогда ответ на наш вопрос:
нули функции достигаются при
x = {-2; -1; 1; 2}
2)
f(x) = 0 когда
либо (х² - 4) = 0 либо
при любом х.
Значит, наши нули получаются только при условии (х² - 4) = 0 .
Таким образом, нули функции достигаются при
х = ±2
Похожие вопросы
Предмет: Қазақ тiлi,
автор: shonkakapash
Предмет: Английский язык,
автор: m68278722
Предмет: Українська література,
автор: nightsniper29052011
Предмет: Физика,
автор: metachok1
Предмет: Математика,
автор: flamythunder