Предмет: Алгебра,
автор: IniSai
20 баллов. помогите пожалуйста. срочно. полное, подробное решение.
Приложения:
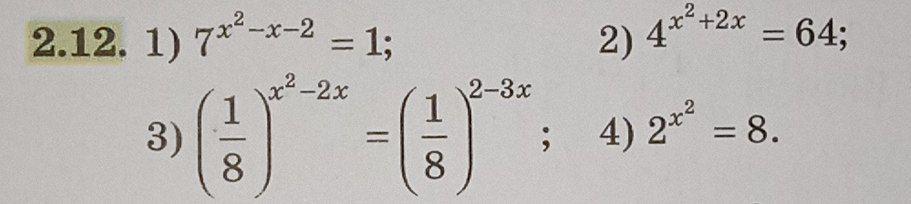
Ответы
Автор ответа:
2
Ответ:
1) -1; 2; 2) -3; 1; 3) -2; 1; 4) -√3; √3.
Объяснение:
Решить уравнения:
- Если степени равны, их основания равны, то и равны их показатели.
Ответ: -1; 2.
Ответ: -3; 1.
Ответ: -2; 1.
Ответ: -√3; √3.
#SPJ1
Похожие вопросы
Предмет: Английский язык,
автор: titil22823
Предмет: Английский язык,
автор: lolidkandidc0
Предмет: Русский язык,
автор: nezukoonishan
Предмет: Математика,
автор: kausar199821
Предмет: Математика,
автор: kausar199821