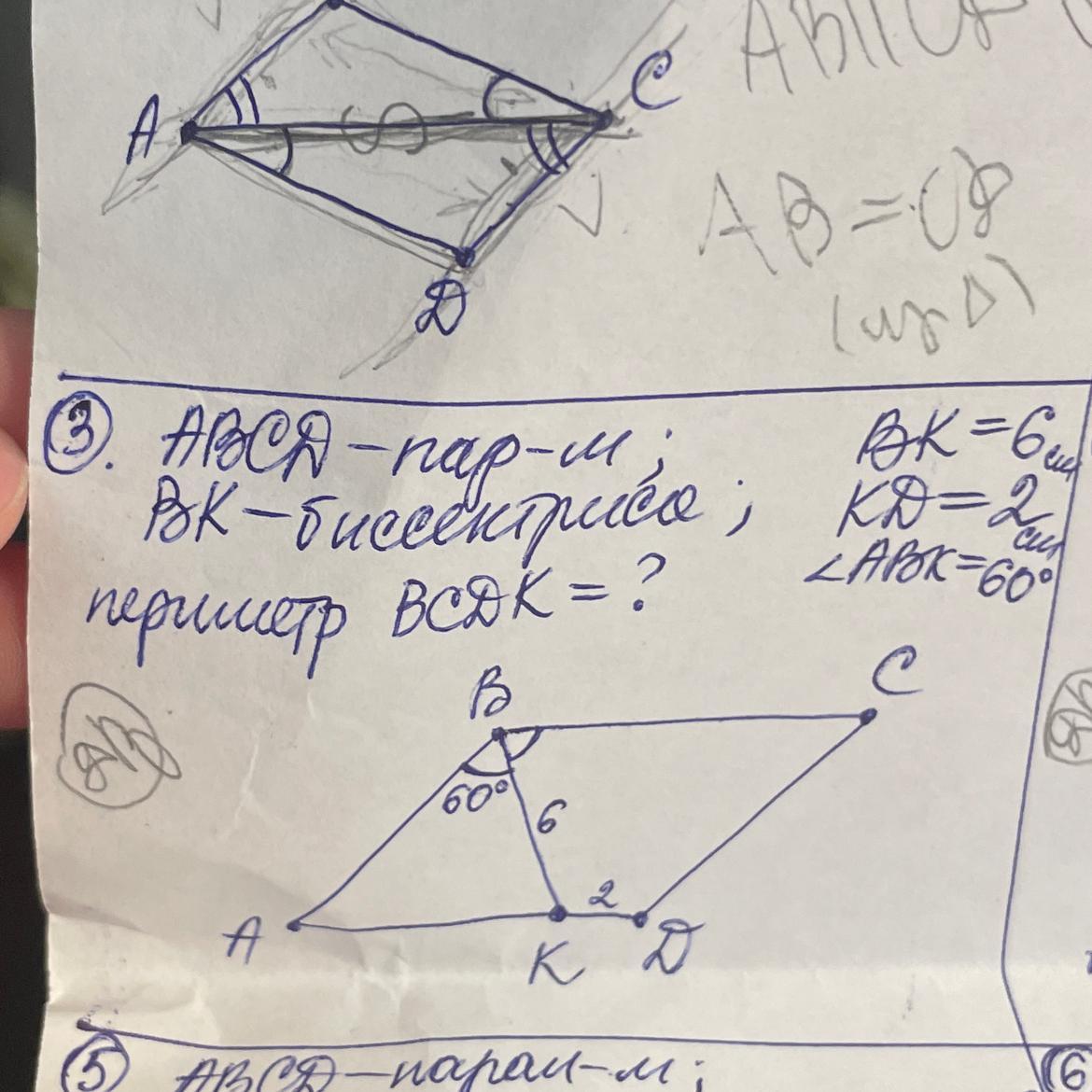
ABCD-параллелограмм
BK-биссектриса
BK=6см
KD=2см
угол AKB=60градусов
периметр BCDK-?
Ответы
Ответ:
Биссектриса ВК отсекает от параллелограмма равнобедренный треугольник,где
АВ=АК,а углы при основании равны между собой
<АВК=<АКВ=60*
Узнаем угол А треугольника АВК
<А=180-60•2=60*
Треугольник АВК не равнобедренный,он равносторонний,т к все его три угла по 60*,а это значит
АВ=АК=ВК=6 см
А т к противоположные стороны параллелограмма равны между собой и параллельны,то
АВ=СD=6 см
Противоположные углы параллелограмма тоже равны между собой
<А=<С=60*
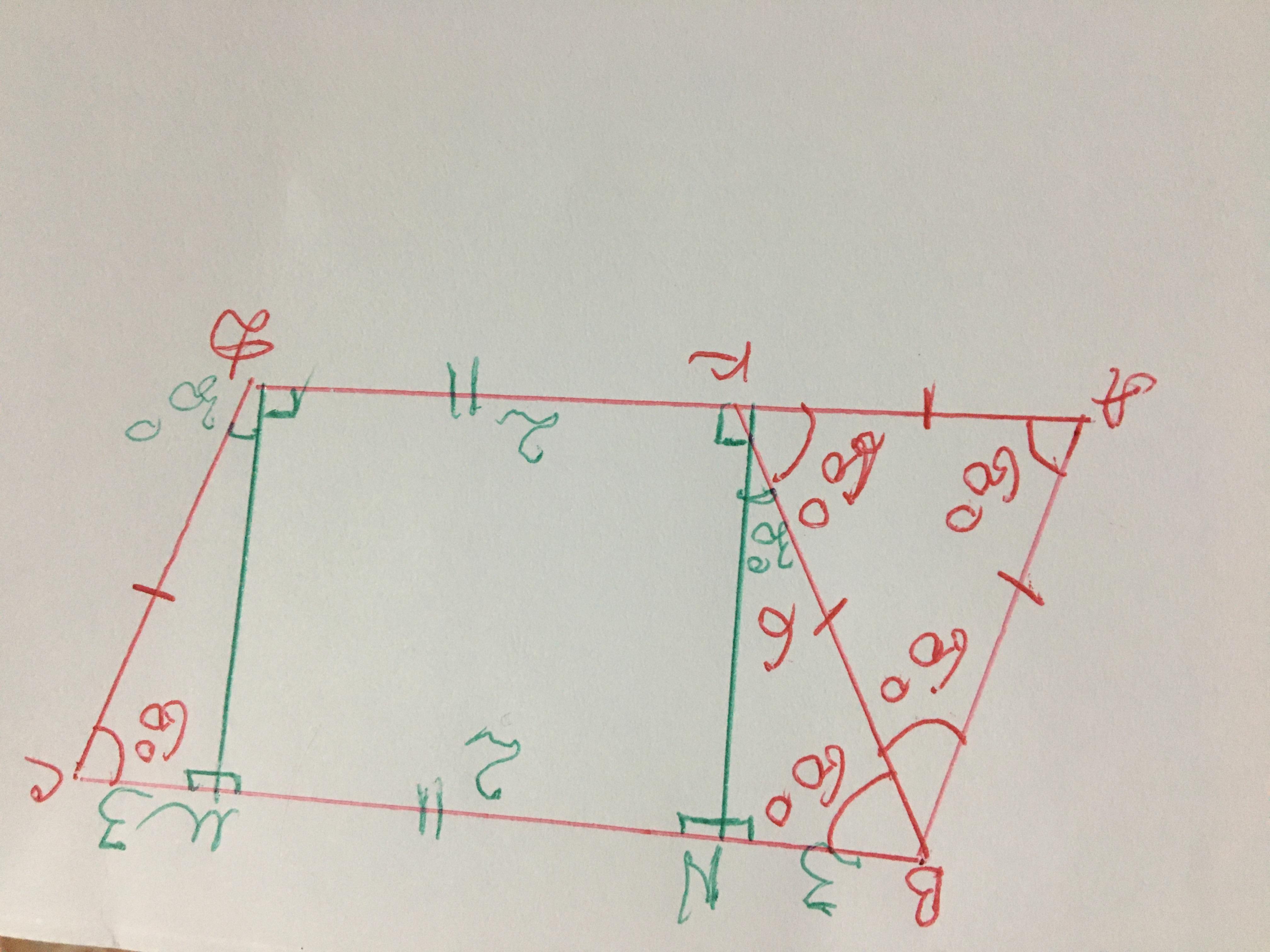
Теперь посмотрим,что из себя представляет четырёхугольник ВСDK
Оказывается-это равнобедренная трапеция,т к ВК=СD,ВС || KD, и
углы при бОльшем основании
равны между собой
<С=<КВС=60*
Узнаем углы при меньшем основании трапеции
К боковой стороне трапеции прилегают углы,Сумма которых равна 180*
<ВКD=180*-60*=120*
<CDK=180*-60*=120*
Проведём в трапеции 2 высоты
Высота-перпендикуляр на основание ВС,образует прямые углы
<ВNK=<KNM=<DMN=<DMC=90*
<NKD=<MDK=90*, тогда
<ВКN=<CDM=120*-90*=30*
И высота отсекает от трапеции два равных прямоугольных треугольника
Рассмотрим один из них
Треугольник ВКN
Катет ВN лежит напротив угла 30 градусов,а это значит,что катет ВN в два раза меньше гипотенузы ВК
Катет ВN=6:2=3 см
ВС=АD=3+2+3=8 см
Р ВСDK=2+8+6•2=22 см
Объяснение:
Можно было решить гораздо проще
<АКВ=<КВС=60*,как накрест лежащие при ВС || АD и секущей ВК
<А=180-60•2=60*
Треугольник АВК равносторонний,т к в нем все углы по 60*,значит и стороны равны между собой
АВ=ВК=АК=6 см
Противоположные стороны параллелограмма равны между собой АВ=СD=6 см
АD=BC=6+2=8 см
Р ВСDK=6•2+8+2=22 см