Предмет: Алгебра,
автор: Viscount
Докажите тождество и найдите значение выражения
Приложения:

Ответы
Автор ответа:
1
Ответ:
6) Доказать тождество .
Применяем формулу разности квадратов и тригонометрическую единицу . Причём из следует равенство
7) Найти значение выражения .
Приложения:
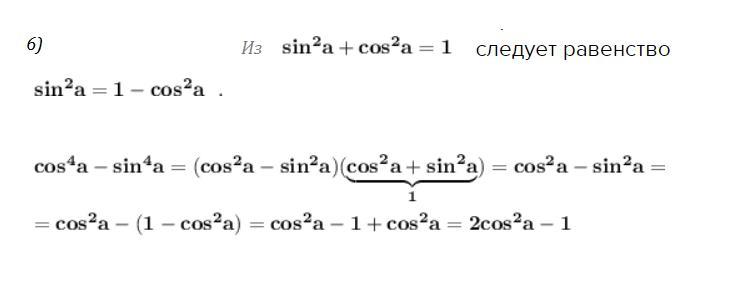
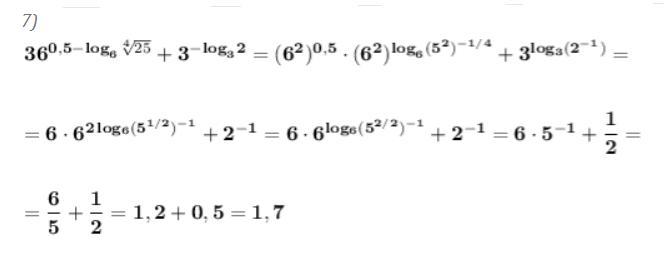
Viscount:
Нижайше благодарю
Посмотрите ещё раз, исправила описку
Похожие вопросы
Предмет: Английский язык,
автор: zpeppppp
Предмет: Биология,
автор: sb99d6j27k
Предмет: Українська література,
автор: pavlovdenis966
Предмет: Английский язык,
автор: jenanalaa6339
Предмет: Математика,
автор: andriypolak