Question

Срочно помогите 2 задачки , даю 70 баллов

Answer 1

Ответ:

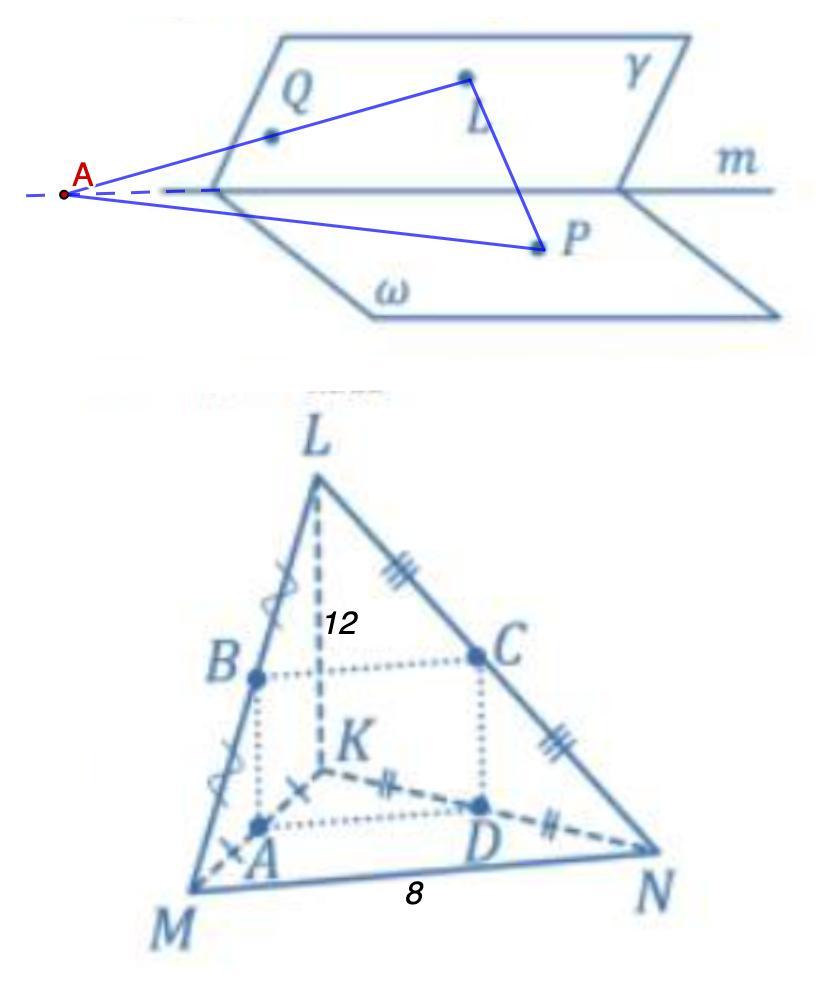
1) PQL ∩ γ = AL; PQL ∩ ω = AP.

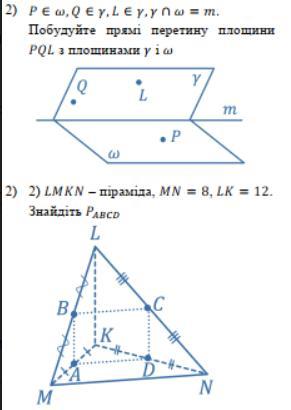
2) P(ABCD) = 20.

Объяснение:

1) Р ∈ ω, Q ∈ γ, L ∈ γ, γ ∩ ω = m. Постройте прямые пересечения плоскости РQL c плоскостями γ и ω

2) LMKN - пирамида, MN = 8, LK = 12. Найти Р(АВСD).

1) Дано: Р ∈ ω, Q ∈ γ, L ∈ γ, γ ∩ ω = m.

Построить: прямые пересечения плоскости РQL c плоскостями γ и ω.

Решение:

Q ∈ γ, L ∈ γ ⇒ Q и L соединяем.

• Линия пересечения двух плоскостей принадлежит обеим плоскостям.

QL ∩ m = A

A ∈ ω; P ∈ ω ⇒ A и Р соединяем.

• Через две пересекающиеся прямые можно провести плоскость, причем только одну.

Получили плоскость PQL.

AL ⊂ γ; AL ⊂ PQL ⇒ PQL ∩ γ = AL

AP ⊂ ω; AP ⊂ PQL ⇒ PQL ∩ ω = AP

2) Дано: LMKN - пирамида,

MN = 8, LK = 12.

MB = BL; NC = CL; MA = AK; ND = DK.

Найти: Р(АВСD)

Решение:

1. Рассмотрим ΔMLN.

MB = BL; NC = CL ⇒ BC - средняя линия.

Средняя линия параллельна стороне, которую она не пересекает, и равна ее половине.

⇒ ВС || MN; BC = MN : 2 = 4

2. Рассмотрим ΔMKN.

MA = AK; ND = DK ⇒ AD - средняя линия.

AD || MN; AD = MN : 2 = 4

3. Рассмотрим ΔKLN.

NC = CL; ND = DK ⇒ DC - средняя линия.

DC = KL : 2 = 6

4. Рассмотрим ABCD.

ВС || MN; AD || MN.

• Если две прямые параллельны третьей, то они параллельны между собой.

⇒ ВС || AD.

ВС = AD = 4

• Если в четырехугольнике две противоположные стороны равны и параллельны, то это параллелограмм.

⇒ ABCD - параллелограмм.

• Периметр параллелограмма равен удвоенной сумме смежных сторон.

P(ABCD) = 2(BC + CD) = 2(4 + 6) = 20.

#SPJ1