Предмет: Алгебра,
автор: SeverysSnape1
ДОПОМОЖІТЬ ДАЮ 50 БАЛІВ, ВИРІШИТИ НА РІВНІ 9 КЛАСУ
Приложения:
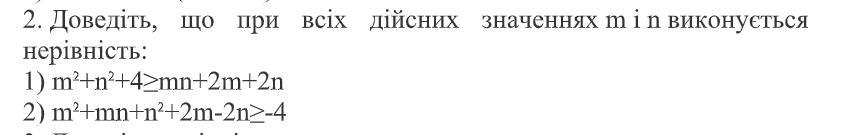
Ответы
Автор ответа:
0
Ответ:
Объяснение
в обоих неравенствах будет выполнять неравенство так как квадраты растут быстрее чем произведения m*n
Автор ответа:
2
1)
сума від’ємних чисел є невід’ємним числом
2)
сума від’ємних чисел є невід’ємним числом
Похожие вопросы
Предмет: Английский язык,
автор: mashappq
Предмет: Литература,
автор: dianamiouw
Предмет: Литература,
автор: dianamiouw
Предмет: Английский язык,
автор: m6249567646
Предмет: Русский язык,
автор: smpleloading