Предмет: Алгебра,
автор: saida3175
сократите дробь - я уже начал решать, но не понимаю как дальше
Приложения:

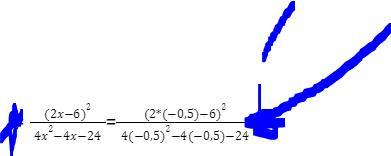
Ответы
Автор ответа:
1
Відповідь:
Пояснення:
Решим уравнение
Подставим x=-0.5
Второй способ, сразу с подставлением x
saida3175:
спасибо, но мне нужен другой способ
Какой другой способ? Есть пример?
на второй фотке. там заменяют все иксы
Добавил в решение другой способ
спасибо большое
Похожие вопросы