Предмет: Алгебра,
автор: masha01021
помогите пожалуйста решить задачу , подробно объясните пожалуйста
Приложения:
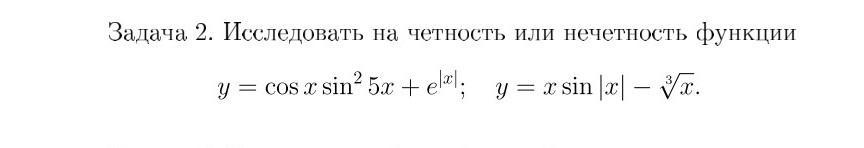
Ответы
Автор ответа:
0
Ответ:
Функция чётна, если f(-x) = f(x) .
Функция y=cosx - чётная функция, поэтому cos(-x) = cosx .
Функция y=sinx - нечётная функция , поэтому sin(-5x) = -sin5x
Функция y = |x| - чётная функция , поэтому | -x | = | x | .
Заданная функция чётная .
Функция нечётна , если f(-x) = -f(x) .
Заданная функция нечётная .
Приложения:

masha01021:
спасибо большое
если будет время помогите на другие задачи вы хорошо объясните
Похожие вопросы
Предмет: Алгебра,
автор: gorshkovan599
Предмет: Физика,
автор: k91239515
Предмет: Українська мова,
автор: fgertys
Предмет: Английский язык,
автор: max2003672
Предмет: Информатика,
автор: kukushka2281337996