Question

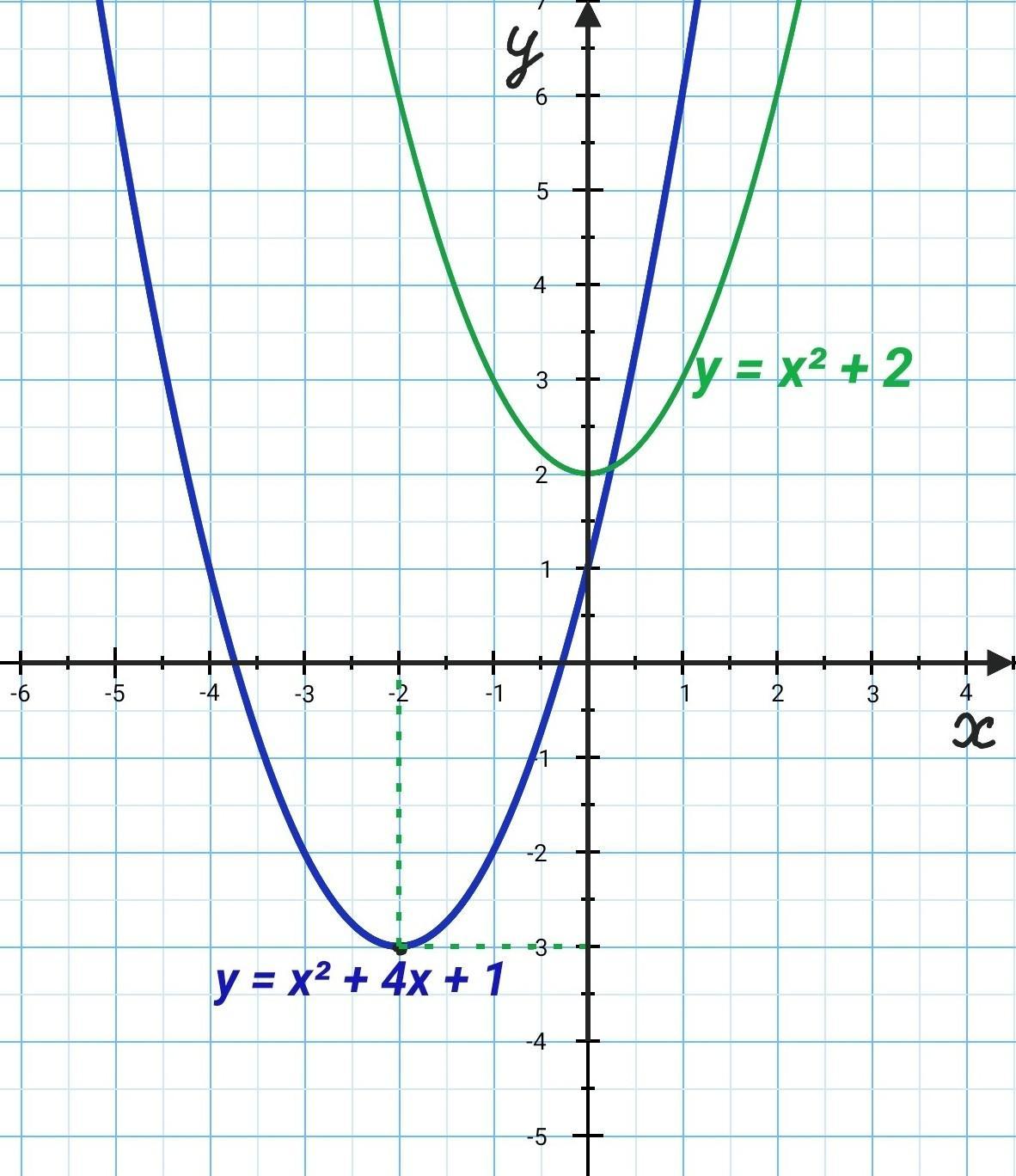
Найдите координаты вершины параболы.(Желательно с картинкой) 1) y = x² + 4x + 1; 2)y=x²+2; ​

Answer 1

Ответ:

Координаты вершины параболы:

1) (-2; -3)

2) (0; 2)

Объяснение:

Найдите координаты вершины параболы. 1) y = x² + 4x + 1; 2)y=x²+2;

• Парабола является графиком квадратичной функции.

Если дана квадратичная функция

у = ах²+ bx + c

то абсциссу вершины параболы $(x_0;y_0)$ можно вычислить по формуле:

$\bf x_0 = \dfrac{ - b}{2a}$

Ординату можно вычислить, подставив полученное значение в формулу данной функции.

Решение

1) у = х² + 4х + 1

а = 1; b = 4.

Тогда:

$x_0= \dfrac{ - 4}{2 \times 1} = \bf - 2$

$y_0 = {( - 2)}^{2} + 4 \times ( - 2) + 1 = 4 - 8 + 1 = \bf- 3$

Вершина параболы: (-2; -3)

2) у = х² + 2

а = 1; b = 0.

$x_0= \dfrac{ 0}{2 \times 1} = \bf 0$

$y_0 = {0}^{2} + 2 = \bf 2$

Вершина параболы: (0; 2)

#SPJ1