Предмет: Математика,
автор: 20232024
Буду очень благодарна, если ответ будет дан с решением
Приложения:
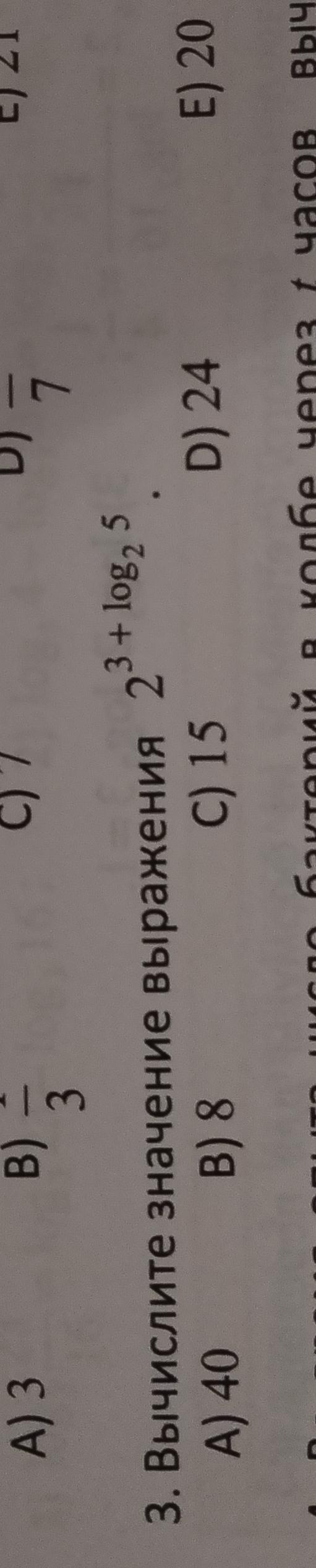
Ответы
Автор ответа:
1
Есть выражение
Мы можем переписать это как , используя свойство степеней, которое гласит:
Теперь мы можем применить свойство логарифмов к второму члену этого произведения. Это дает нам
равно 8, поэтому выражение становится
равно 40.
Значение выражения равно 40
Ответ: A) 40
20232024:
Огромное-преогромное спасибо Вам!
Похожие вопросы
Предмет: Українська мова,
автор: polinamhailovvaa
Предмет: Математика,
автор: gashalive622
Предмет: Українська мова,
автор: stalmaria4
Предмет: Математика,
автор: DrakoGirl
Предмет: Математика,
автор: robloxpromocodes07