Предмет: Математика,
автор: roman4iku
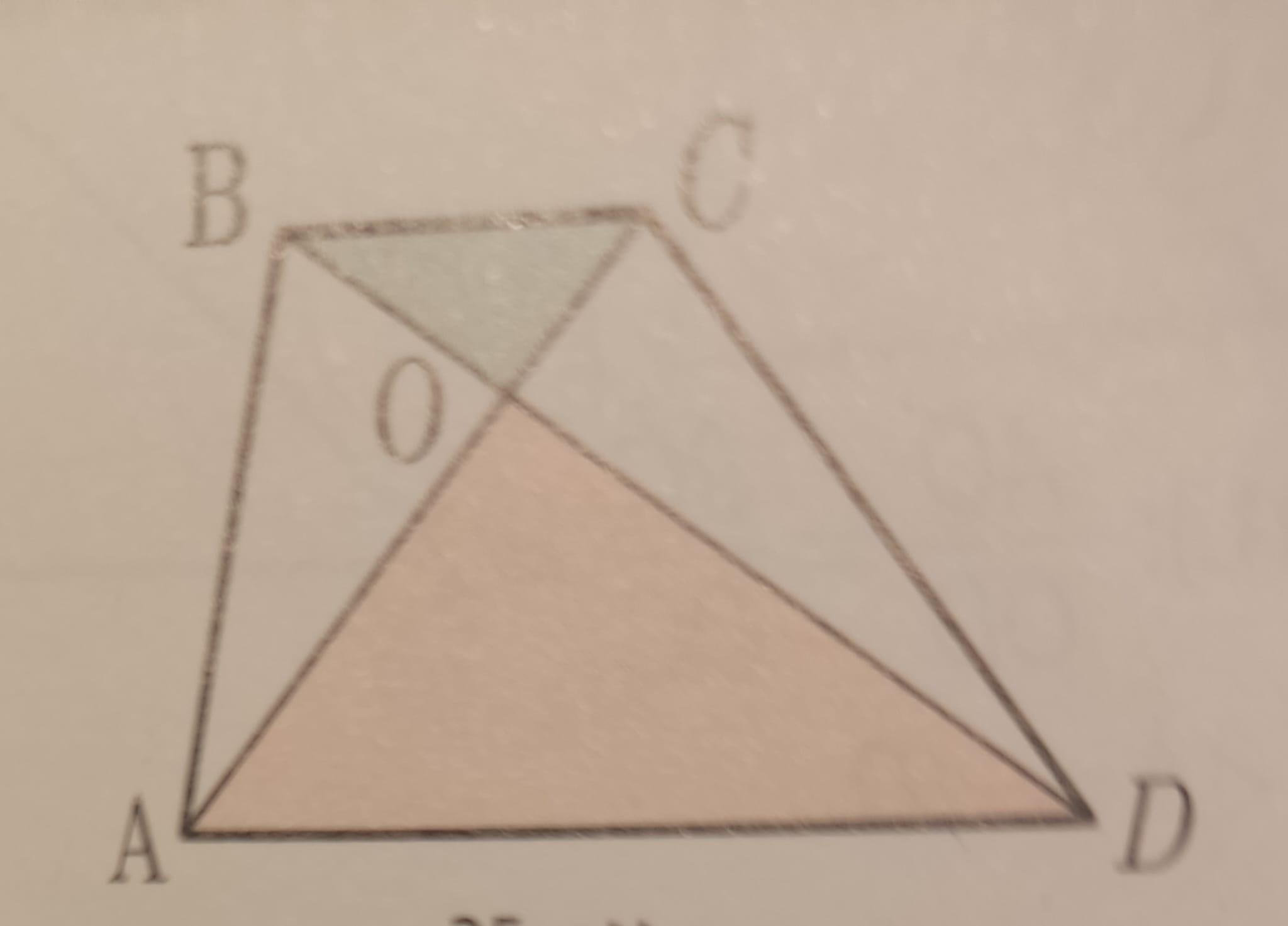
Дано: ABCD – трапеция.
Доказать:
а) ▲BOC ~ ▲DOA
б) BC/AD=BO/OD
Приложения:
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
1) рассмотрим ΔВОС и ΔDОА.
∠ВОС = ∠DOA как вертикальные,
∠ВСО = ∠ODA как накрест лежащие при параллельных прямых
ВC и AD (т.к. АВСD - трапеция по условию) и секущей АС.
1признак подобия Δ-ков:
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны. Cледовательно,
ΔВОС ~ ΔDОА, ч.т.д.
2) Подобные Δ-ки — это Δ-ки, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника. Исходя из определения подобных Δ-ков, получаем,что
ВС/AD = BO/OD/
Похожие вопросы
Предмет: Русский язык,
автор: ajaruorazymbet
Предмет: География,
автор: ggmml
Предмет: Литература,
автор: mirasikundu
Предмет: Русский язык,
автор: denismashoshin2020
Предмет: Математика,
автор: amiina0708