Предмет: Математика,
автор: rodzia
Знайти найбільше та найменше значення функції
Приложения:
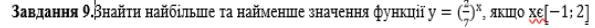
Ответы
Автор ответа:
0
Можемо знайти найбільше та найменше значення функції, підставивши границі інтервалу в функцію.
Функція є спадаючою (a>1) на всій області визначення, тому:
Найбільше значення функції досягається при найменшому значенні , тому ми підставимо
в функцію:
Найменше значення функції досягається при найбільшому значенні , тому ми підставимо
в функцію:
Отже, найбільше значення функції на даному інтервалі дорівнює , а найменше -
.
Похожие вопросы
Предмет: Математика,
автор: alnurnurzanuly27
Предмет: Қазақ тiлi,
автор: z8886718
Предмет: Химия,
автор: Ushsi
Предмет: Математика,
автор: rasulrasulov539
Предмет: История,
автор: 666Yanderkun999