Предмет: Математика,
автор: sasagrinev16
Знайти проміжки зростання та спадання функції у=х³-3х2-9х-1
Ответы
Автор ответа:
0
Ответ:
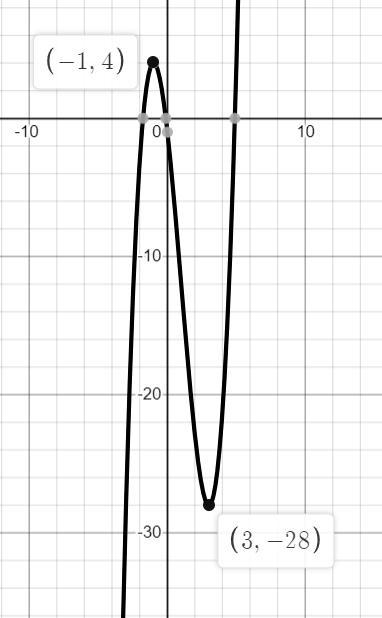
функция возрастает на промежутках (-∞;-1] и [3;+∞)
функция убывает на промежутке [-1;3]
Пошаговое объяснение:
Промежутки убывания и возрастания функции ищем при помощи первой производной.
Ищем нули функции
Нули функции х₁ = -1; х₂ = 3.
Таким образом мы получили промежутки
(-∞;-1] [-1;3] [3;+∞)
(-∞;-1] возьмем, например, х = -2
y'(-2) = 3*(-2)² - 6*(-2) -9 = 15 > 0 функция возрастает.
[-1;3] возьмем х=0
y'(0) = -9 < 0 функция убывает.
[3;+∞) пусть х = 4
y'(4) = 3*4² - 6*4 - 9 = 15 > 0 функция возрастает.
чтобы не сомневаться, вот график функции
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: barylomaksim
Предмет: Биология,
автор: kirillkiev2010
Предмет: Алгебра,
автор: veronishna99
Предмет: Русский язык,
автор: sabinadelamo