Предмет: Другие предметы,
автор: brutyannona0
ПОМОГИТЕ ПОЖАЛУЙСТА!! СРОЧНО: задача доказать уравнение на картинке методом индукции.
Приложения:
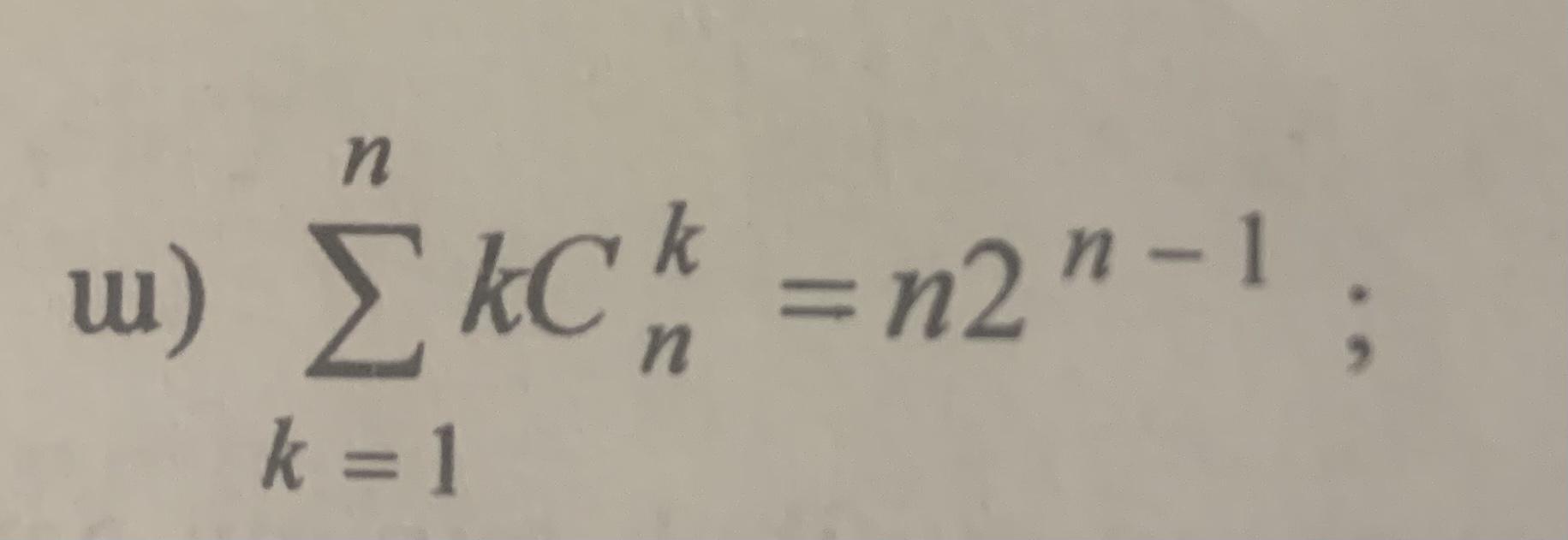
Ответы
Автор ответа:
0
База индукции
Проверим уравнение для :
Справа:
Таким образом, уравнение верно для .
Шаг индукции
Предположим, что уравнение верно для :
Теперь докажем, что уравнение верно для :
Разделим сумму на две части:
Используя свойство биномиальных коэффициентов , получим:
Раскроем скобки и перегруппируем слагаемые:
Первая сумма становится:
Вторая сумма равна по предположению индукции.
Третье слагаемое равно .
Таким образом, получаем:
Сгруппируем слагаемые:
Последнее равенство можно упростить до:
Таким образом, уравнение верно для , если оно верно для
.
Таким образом, уравнение верно для всех натуральных по принципу математической индукции.
brutyannona0:
Объясните пожалуйста с «Раскроем скобки и перегруппируем слагаемые:» более подробно.
Похожие вопросы
Предмет: История,
автор: zxjs
Предмет: Алгебра,
автор: valeriya5677
Предмет: Информатика,
автор: vova26277272
Предмет: Математика,
автор: eveirdas