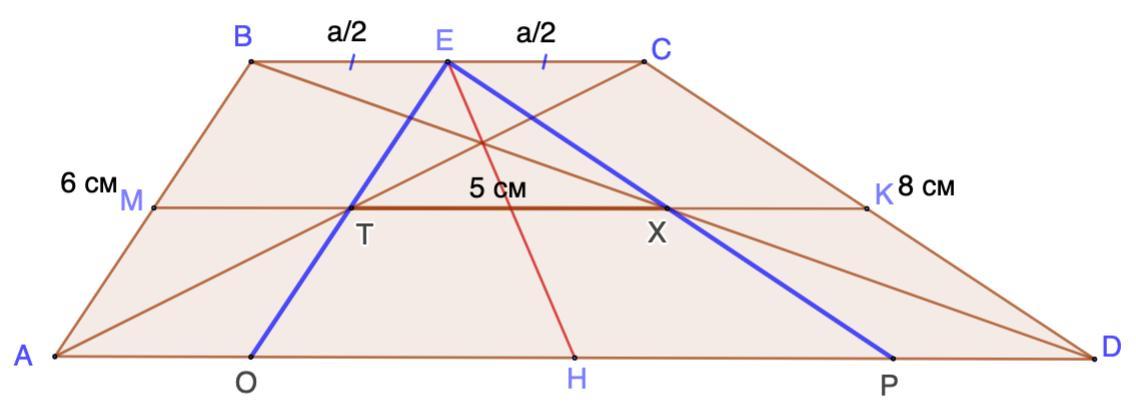
Цікаві задачі для учнів неледачих 66. Бічні сторони трапеції дорівнюють 6 см і 8 см, а відстань між серединами її діагоналей дорівнює 5 см. Знайдіть відстань між серединами основ трапеції.
Ответы
Ответ:
Расстояние между серединами оснований трапеции равно 5 см.
Объяснение:
Боковые стороны трапеции равны 6 см и 8 см, а расстояние между серединами ее диагоналей равно 5 см. Найдите расстояние между серединами оснований трапеции.
Дано: ABCD - трапеция;
АВ = 6 см; CD = 8 см;
АТ = ТС; ВХ = ХD;
ТХ = 5 см;
ВЕ = ЕС; АН = НD.
Найти: EH.
Решение:
Проведем через точку Е прямые ЕО || BA; EP || CD.
Пусть ВС = а, тогда ВЕ = ЕС = а/2 см.
АВЕО - параллелограмм (по определению)
- Противоположные стороны параллелограмма равны.
⇒ ВЕ = АО = а/2 см, АВ = ОЕ = 6 см
ECDP - параллелограмм (по определению)
⇒ ЕС = PD = a/2 см; ЕР = CD = 8 см.
Рассмотрим ΔBCD.
BX = XD; XK || BC ⇒ XK = средняя линия.
- Средняя линия равна половине стороны, которую она не пересекает.
⇒ ХК = а/2 см
Рассмотрим ΔАСD.
ТК - средняя линия.
ТК = 5 + а/2 (см)
⇒ AD = 2TK = 10 + a (см)
ОР = AD - АО - PD = 10 + a - a/2 - a/2 = 10 (см)
Рассмотрим ΔОЕР.
ОЕ = 6 см, ЕР - 8 см, ОР = 10 см.
Получили Пифагорову тройку.
То есть
ОР² = ОЕ² + ЕР²
100 = 36 + 64
⇒ ΔОЕР - прямоугольный.
- Сумма острых уголов прямоугольного треугольника равна 90°.
⇒ ∠ЕОР + ∠ЕРО = 90°
∠ЕОР = ∠А (соответственные при АВ || OE и секущей AD)
∠ЕРО = ∠В (соответственные при CD || EP и секущей AD)
⇒ ∠A + ∠D = 90°
- Если сумма углов в трапеции при основании равна 90 градусов, то длина отрезка, соединяющего середины оснований, равна полуразности длин оснований.
⇒ ЕН = (AD - BC) : 2 = (a + 10 - a) : 2 = 5 (см)
⇒ расстояние между серединами оснований трапеции равно 5 см.
#SPJ1