Предмет: Математика,
автор: fuzey5721
Cрочно даю 100 балов Знайдіть f /(А), якщо:
Приложения:
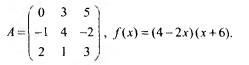
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Для початку, знайдемо похідну функції .
Застосуємо правило похідної добутку: , де
і
.
Тоді і
.
Отже, похідна функції буде:
Тепер, щоб знайти , ми підставимо матрицю
в отриману похідну. Оскільки
є лінійною функцією, ми можемо застосувати її до кожного елемента матриці
окремо:
,
де - одинична матриця.
Тоді отримаємо:
.
.
.
Отже, .
fuzey5721:
АОАОАОАО Дяк)
Похожие вопросы
Предмет: География,
автор: nadezhdachertushkina
Предмет: Физика,
автор: veronictilop
Предмет: Алгебра,
автор: milanA456677
Предмет: Математика,
автор: DaniksAST