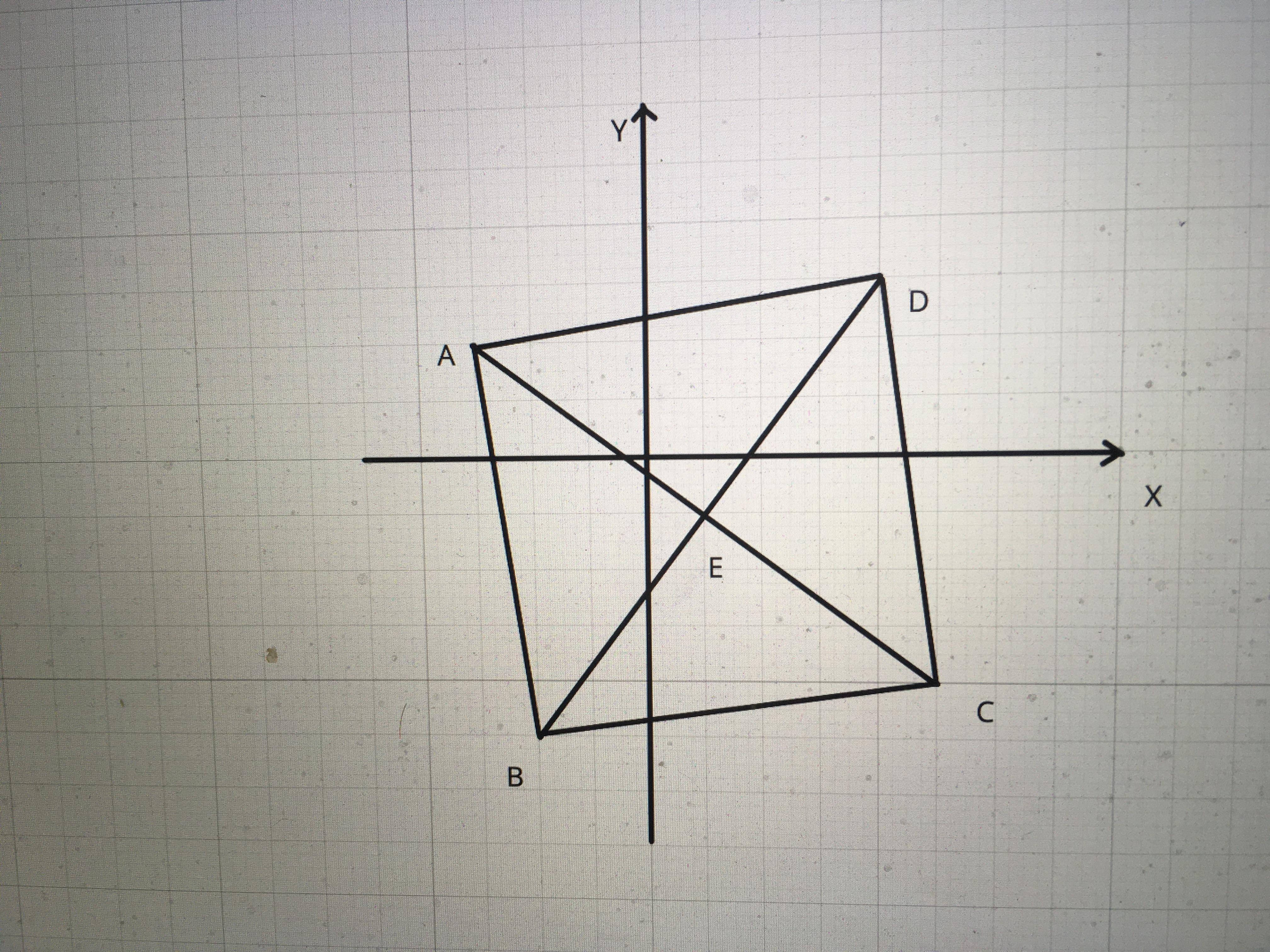
Помогите с решением пожалуйста

Ответы
АС={(5-)-3; -4-2}={8;-6}
|AC|^2=64+36=100
|AC|=10
Значит сторона квадрата AB=10/√2=5√2
Пусть В={x;y}
AB={x-(-3);y-2}={x+3;y-2}
BC={5-x;-4-y}
У квадрата стороны равны, |AB|=|AC|=5√2
|AB|^2]=|BC|^2
(x+3)^2+(y-2)^2=50
(5-x)^2+(y+4)^2=50
это система
x=4;y=3
это координаты точки В
Координаты O
O={(-3+5)/2;(2-4)/2)={1;-1}
О середина ВD , пусть D(x1;y1}
тогда 1=(4+x1)/2; x1=-2
-1=(3+y1)/2; y1=-5
D={-2;-5}
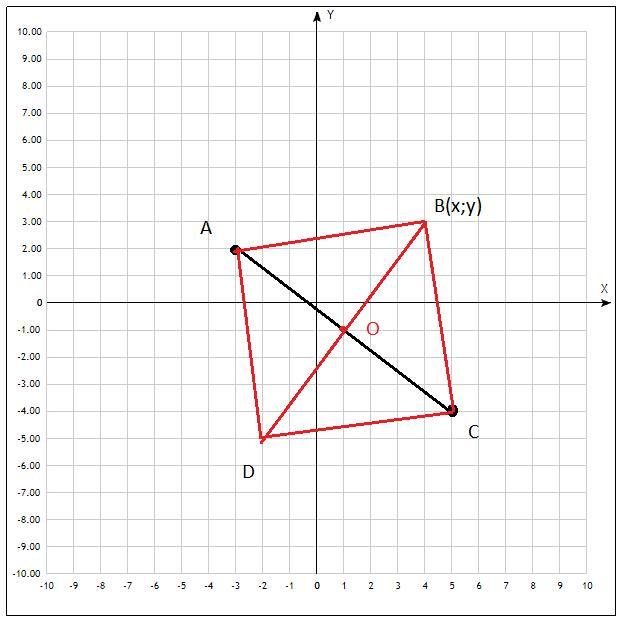
https://znanija.com/task/1022542?utm_source=android&utm_medium=share&utm_campaign=question
Ответ:
(-2;-5); (4;3).
Объяснение:
Предварительное важное замечание. Пусть нам дан вектор {a;b}, отложенный от начала координат. Оказывается, если мы хотим повернуть этот вектор на 90° относительно начала координат против часовой стрелки, надо поменять местами координаты вектора, и у получившейся первой координаты поменять знак - получится вектор {-b,a}. Объяснить это можно совсем просто - если повернуть всю плоскость на 90°, ось OX станет осью OY (поэтому первая координата вектора при повороте станет второй координатой повёрнутого вектора), а ось OY - осью OX, только она будет идти не слева направо, а справа налево (поэтому вторая координата вектора при повороте станет первой координатой повёрнутого вектора, только знак поменяется). Если же мы вектор поворачиваем по часовой стрелке, получится вектор {b;-a}.
Переходим к решениюзадачи. Даны противоположные вершины A(-3;2) и C(5;-4) квадрата. Находим центр квадрата - это точка E, являющаяся серединой отрезка [A;C], поэтому её координаты являются полусуммами соответствующих координат концов отрезка (иными словами, средними арифметическими этих координат):
Найдем координаты вектора EA, вычитая из координат конца вектора координаты его начала:
Считая, что этот вектор отложен из начала координат, видим, что при повороте на 90° в одну и другую сторону возникают векторы
{-3;-4} и {3;4}.
Чтобы получить вершины B и C квадрата, остаётся отложить эти векторы из точки E; их концы и будут требуемыми вершинами. Как известно, координаты конца вектора получаются из координат его начала добавлением соответствующих координат вектора, поэтому
Если нумерация вершин квадрата происходила не против часовой стрелки, а по часовой, координаты вершин B и D нужно поменять:
B(4;3); D(-2;-5).