допоможіть, будь ласка, взагалі не можу зрозуміти(
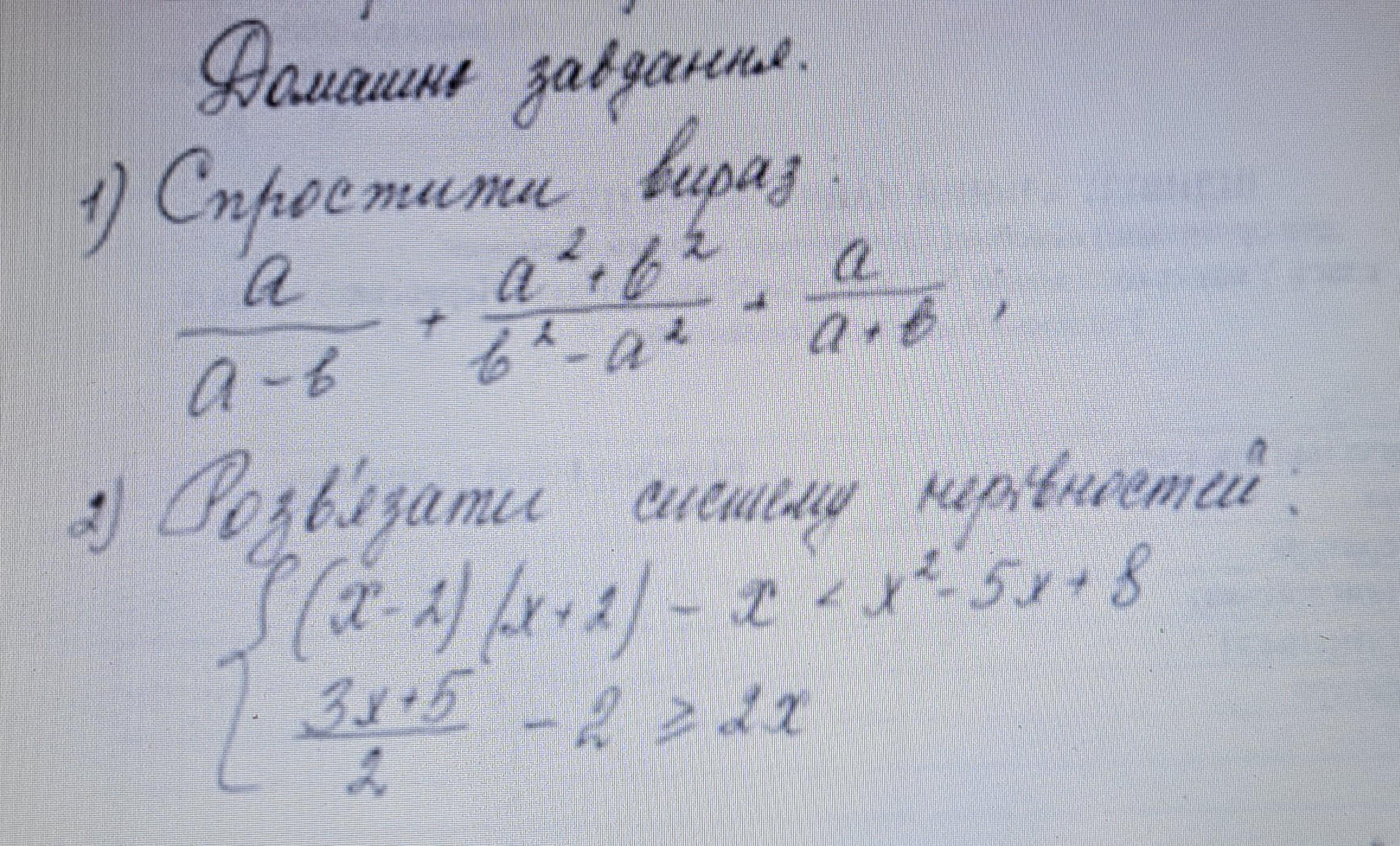
Ответы
Ответ:
1)
2) та
Пошаговое объяснение:
1) Для спрощення даного виразу, спочатку знайдемо спільний знаменник для всіх дробів. Зауважимо, що знаменником першої та третьої дробі є , а знаменником другої дробі є
. Оскільки
можна розкласти як
, то можемо записати:
Тепер знаменники всіх дробів однакові. За допомогою спільного знаменника, можемо скласти чисельники дробів:
Тепер спростимо чисельник:
Отримали спрощений вираз
2) Для розв'язання даної системи нерівностей, розглянемо кожну нерівність окремо:
a)
Спочатку розкриємо дужки:
Скоротимо подібні члени:
Перенесемо всі члени на одну сторону:
Розділимо обидві частини на 6:
Спрощуємо дріб:
Таким чином, розв'язанням першої нерівності є .
б)
Спочатку виконаємо рівняння в дужках:
Перенесемо всі члени на одну сторону:
Змінимо напрямок нерівності, оскільки множник 2 в знаменнику є позитивним числом:
Перенесемо всі члени на одну сторону:
Змінимо напрямок нерівності та помножимо обидві частини на -1, щоб змінити знак:
Таким чином, розв'язанням нерівності є .
Отже, розв'язком системи нерівностей є та
.