Question

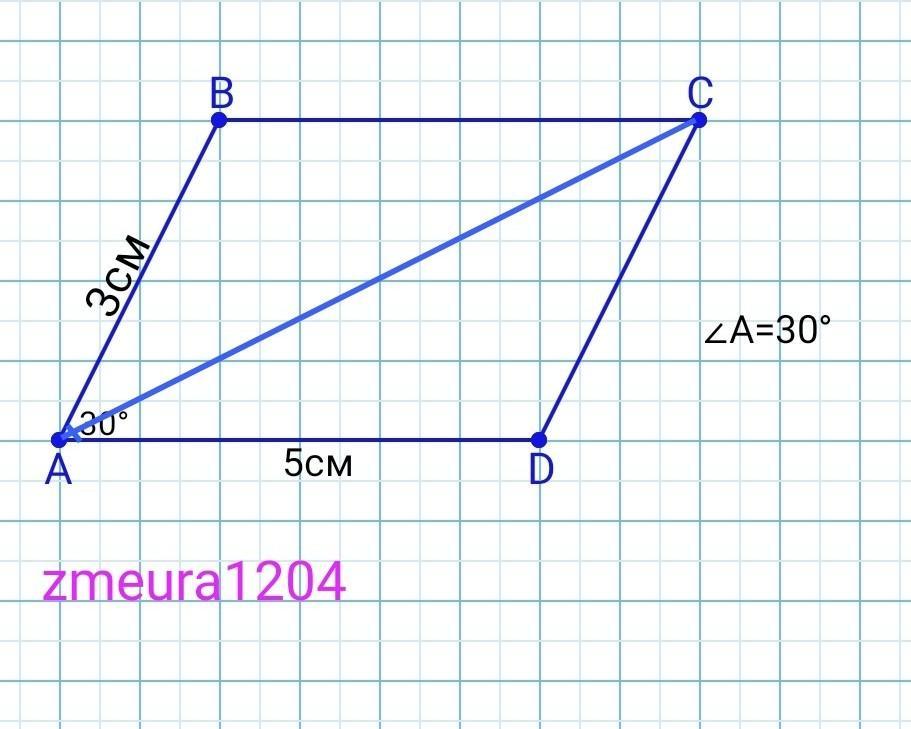
Дві сторони паралелограма дорівнюють 3 см і 5 см, а кут 30°. Знайдіть: між ними 1) більшу діагональ паралелограма; 2) площу паралелограма. СРОЧНО​

Answer 1

Ответ:

Площа дорівнює 7,5см²

Діагональ дорівнює ≈2,8см

Объяснение:

AB=3см

BC=5см

∠A=30°

AC=?

S(ABCD)=?

Розв'язання:

S(ABCD)=AB*AD*sin∠A=

=3*5*sin30°=15*½=7,5см²

Сума кутів прилеглих до однієї сторони паралелограма дорівнює 180°.

∠В=180°-∠А=180°-30°=150°

Більша діагональ лежить проти тупого кута паралелограма.

За теоремою косинусів:

АС=√(АВ²+ВС²-2*АВ*ВС*cos∠B)=

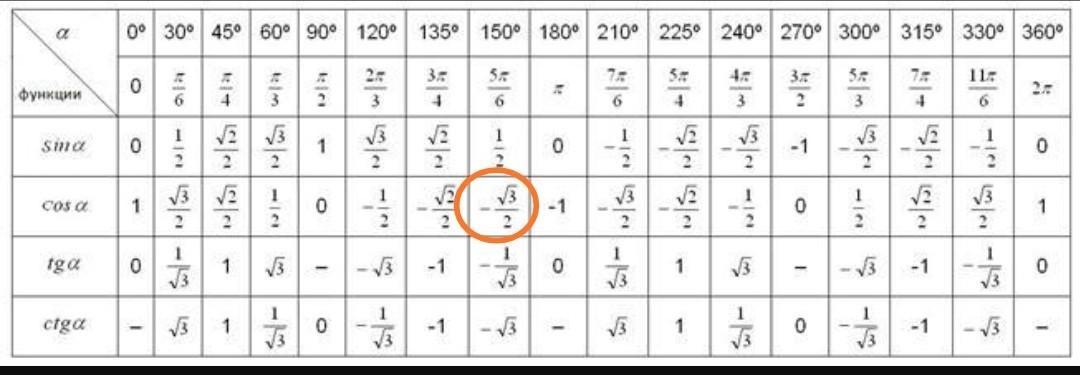
=√(3²+5²-2*3*5*cos150°)=

=√(9+25-2*15*(-√3/2))=

=√(34+15√3)≈√(34-26)≈√8≈

≈2√2≈2,8см