Предмет: Геометрия,
автор: vasika71
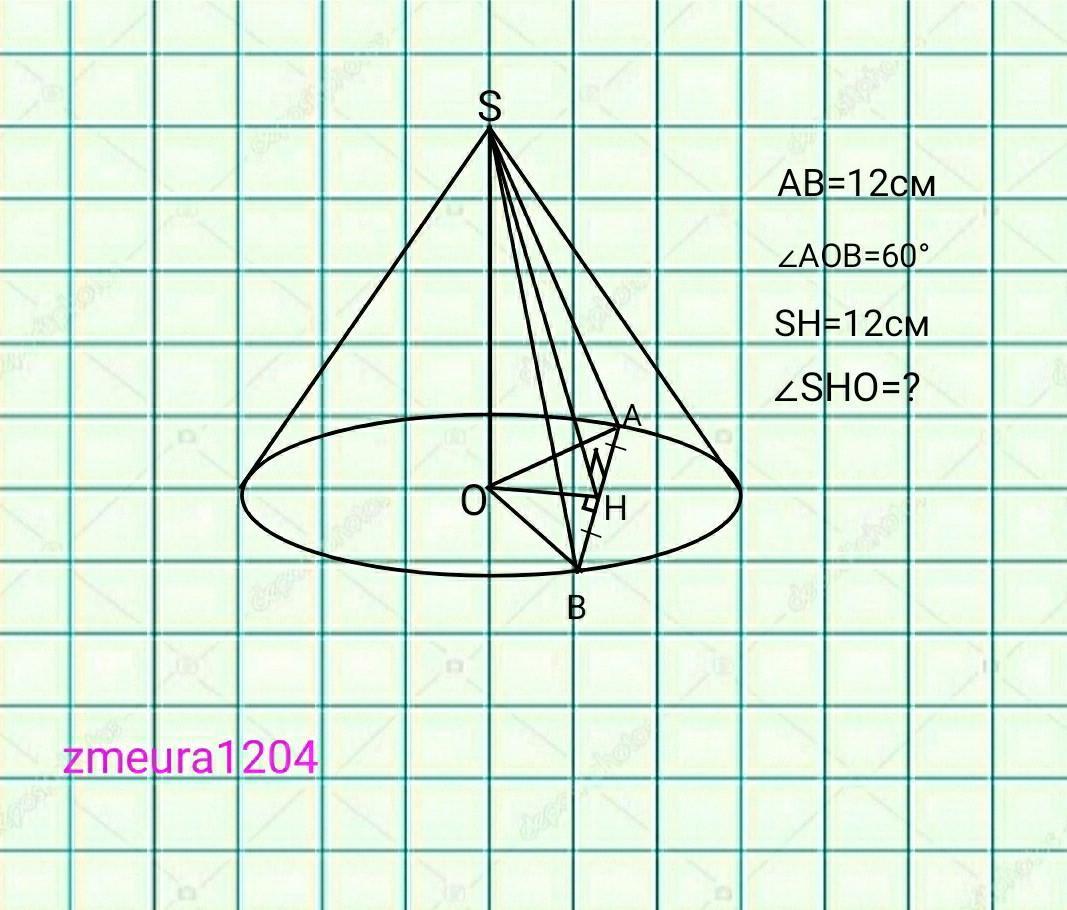
Через вершину конуса проведено переріз, який перетинає його основу по хорді завдовжки 12 см. Ця хорда стягує ду- гу, градусна міра якої дорівнює 60°. Відстань від вершини конуса до цієї хорди дорівнює 12 см. Знайдіть кут між площиною перерізу та площиною основи конуса.
Ответы
Автор ответа:
1
Ответ:
Кут між площиною перерізу та площиною основи дорівнює 30°
Объяснение:
∆OAB- рівносторонній трикутник.
Один із кутів 60°, а сторони ОВ=ОА=R.
OA=OB=AB=12см.
ОН- висота, медіана і бісектриса ∆ОАВ
Формула висоти рівностороннього трикутника h=a√3/2; де а- сторона трикутника.
ОН=АВ√3/2=12√3/2=6√3см.
∆ОSH- прямокутний трикутник.
∠SOH=90°;
SH=12см; ОН=6√3см
За теоремою Піфагора:
SO=√(SH²-OH²)=√(12²-(6√3)²)=6см
Катет SO в два рази менше гіпотенузи SH, тоді він лежить проти кута 30°.
∠ОSH=30°
Сума гострих кутів прямокутного трикутника дорівнює 90°, тоді кут
∠SHO=90°-∠OSH=90°-30°=60°
Приложения:
Похожие вопросы
Предмет: Литература,
автор: 134899
Предмет: Окружающий мир,
автор: granichkate111
Предмет: Математика,
автор: m72817168
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: M1r0r