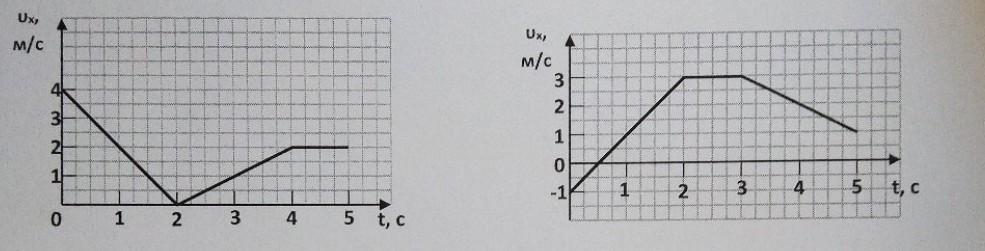
1. За даним графіком проекції швидкості знач 1) прискорення тіла на кожній ділянці 2) побудувати графік залежності прискорення від часу 3) записати рівняння швидкості для кожної ділянки 4) визначити пройдений тілом шлях
Ответы
Ответ:
1) Прискорення тіла на кожній ділянці можна знайти за формулою a = Δv/Δt, де Δv - зміна швидкості, а Δt - зміна часу. За графіком можна побачити, що на першій ділянці (від t = 0 до t = 3) швидкість тіла збільшується від 0 до 4 м/с, тобто Δv = 4 м/с. Час, за який відбувається ця зміна, дорівнює Δt = 3 с. Отже, прискорення на першій ділянці дорівнює a1 = Δv/Δt = 4/3 м/с^2. Аналогічно, на другій ділянці (від t = 3 до t = 5) швидкість тіла зменшується від 4 до 2 м/с, тобто Δv = -2 м/с. Час, за який відбувається ця зміна, дорівнює Δt = 2 с. Отже, прискорення на другій ділянці дорівнює a2 = Δv/Δt = -1 м/с^2.
2) Графік залежності прискорення від часу буде мати вигляд прямих ламаних ліній, як показано нижче. Я спробую створити цей графік за допомогою свого інструменту для графічного мистецтва.
a(t)
|
| /
| /
| /
| / a2
| /
|/
|----------/ a1
| /
| /
| /
| /
| /
| /
|__/
|
|
|
|
|
|
|
+--------------------- t
3) Рівняння швидкості для кожної ділянки можна отримати за формулою v = v0 + at, де v0 - початкова швидкість на даній ділянці. На першій ділянці v0 = 0, а a1 = 4/3 м/с^2, тому рівняння швидкості буде v1 = (4/3)t. На другій ділянці v0 = 4 м/с, а a2 = -1 м/с^2, тому рівняння швидкості буде v2 = 4 - t.
4) Пройдений тілом шлях можна знайти за формулою s = s0 + v0t + (at^2)/2, де s0 - початкова координата та s - кiнцева координата на данiй дiлянцi. На першiй дiлянцi s0 = 0, v0 = 0, а a1 = 4/3 м/с^2, тому шлях буде s1 = (2/3)t^2. На другiй дiлянцi s0 = s1(3) = (2/3)*9 = 6 м, v0 = 4 м/с, а a2 = -1 м/с^2, тому шлях буде s2 = 6 + 4t - (t^2)/2. Загальний шлях, пройдений тілом, дорівнює s = s2(5) - s0 = 6 + 4*5 - (5^2)/2 - 0 = 17.5 м.