Предмет: Математика,
автор: nestval24
Подробное решение, лучше в столбик расписывать.
Приложения:
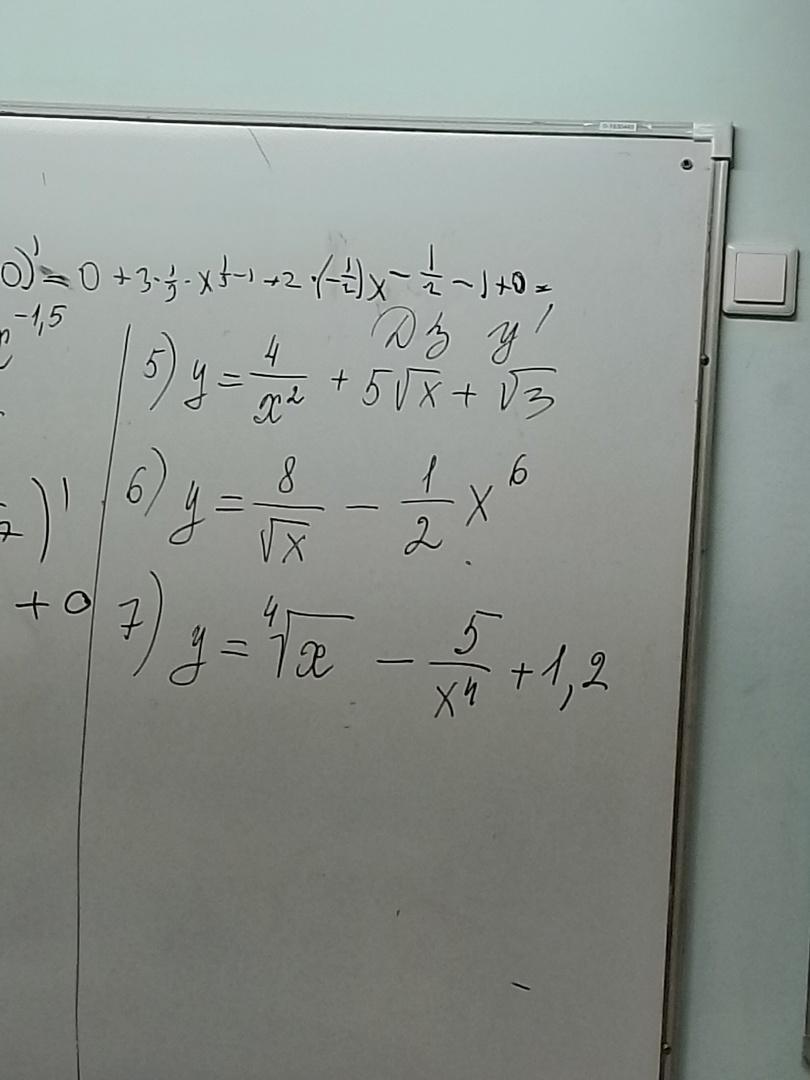
nestval24:
найти y'
Ответы
Автор ответа:
1
Ответ:
Найти производную функции . Применяем правила дифференцирования функций . Используем таблицу производных .
Приложения:


здравствуйте помогите мне пожалуйста, геометрией
Похожие вопросы
Предмет: Геометрия,
автор: Milena1301
Предмет: История,
автор: zlatap279
Предмет: Українська література,
автор: evtodiikira
Предмет: Физика,
автор: valekseevic364