З пункту А в пункт В виїхав велосипедист. Через 2 години назустріч йому вийшов пішохід. Відстань між пунктами дорівнює 69 км. Відомо, що швидкість велосипедиста на 9 км/год більша за швидкість пішохода. Знайти швидкість велосипедиста і швидкість пішохода, якщо до зустрічі велосипедист був у дорозі 5 год.
ДОПОМОЖІТЬ БУДЬ ЛАСКА!! і прохання скорочений запис запишіть в вигляді таблиці..
Ответы
Ответ:
Ми знаємо, що відстань між пунктами А і В дорівнює 69 км. Ми також знаємо, що швидкість велосипедиста (V (В)) на 9 км/год більша, ніж швидкість пішохода (V (П)). І велосипедист був у дорозі 5 годин до зустрічі з пішоходом.
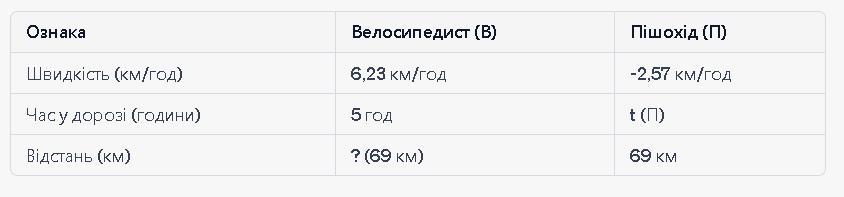
За допомогою таблиці ми можемо сформулювати два рівняння, використовуючи формулу швидкість = відстань / час:
Для велосипедиста:
V (В) = ? (відстань) / 5 год.
Для пішохода:
V (П) = 69 км / t (П).
Ми також знаємо, що швидкість велосипедиста (V (В)) на 9 км/год більша, ніж швидкість пішохода (V (П)), тобто:
V (В) = V (П) + 9 км/год.
Тепер ми можемо створити систему рівнянь на основі цих умов:
1. V (В) = ? / 5
2. V (П) = 69 / t (П)
3. V (В) = V (П) + 9
Ми також знаємо, що велосипедист і пішохід зустрілися через 2 години після того, як велосипедист вирушив. Тобто:
t (П) = t (В) + 2 год.
Зараз ми маємо систему рівнянь, яку можна вирішити для знаходження швидкостей велосипедиста і пішохода, а також часу, який пішохід був у дорозі:
1. V (В) = ? / 5
2. V (П) = 69 / t (П)
3. V (В) = V (П) + 9
4. t (П) = t (В) + 2
Тепер давайте розв'яжемо цю систему рівнянь. Спростимо рівняння 1 і 2:
1. V (В) = ? / 5
2. V (П) = 69 / t (П)
Тепер ми можемо виразити ? відстань у виразі V (В) = ? / 5. Помножимо обидва боки на 5:
? = 5 * V (В)
Тепер ми можемо підставити це значення ? в рівняння 2:
V (П) = 69 / t (П)
Підставимо ? = 5 * V (В):
V (П) = 69 / (5 * V (В))
Далі ми можемо використовувати рівняння 3 для виразу V (П) через V (В):
V (В) = V (П) + 9
Підставимо V (П) з попереднього рівняння:
V (В) = (69 / (5 * V (В))) + 9
Тепер ми маємо одне рівняння з однією невідомою, V (В). Розв'яжемо його:
Спочатку позбавимось від дробу, помноживши обидва боки на 5 * V (В):
5 * V (В) * V (В) = 69 + 45 * V (В)
Розпишемо це рівняння:
5V^2 - 45V - 69 = 0
Тепер ми маємо квадратне рівняння, яке ми можемо розв'язати за допомогою квадратного кореня:
V (В) = (-b ± √(b² - 4ac)) / (2a)
де a = 5, b = -45 і c = -69.
V (В) = (45 ± √((-45)² - 4 * 5 * (-69))) / (2 * 5)
V (В) = (45 ± √(2025 + 1380)) / 10
V (В) = (45 ± √3405) / 10
Для спрощення можемо розкласти 3405 на множники:
V (В) = (45 ± √(225 * 15)) / 10
V (В) = (45 ± 15√15) / 10
Тепер ми маємо два можливих значення для швидкості велосипедиста, одне з позитивним знаком і одне з від'ємним знаком:
1. V (В) = (45 + 15√15) / 10
2. V (В) = (45 - 15√15) / 10
Тепер ми маємо швидкість велосипедиста. Щоб знайти швидкість пішохода, ми можемо використовувати рівняння 3:
V (В) = V (П) + 9
Підставимо значення V (В) з рівнянь 1 і 2:
1. V (В) = (45 + 15√15) / 10
2. V (В) = (45 - 15√15) / 10
Для першого значення V (В):
(45 + 15√15) / 10 = V (П) + 9
V (П) = (45 + 15√15) / 10 - 9
А для другого значення V (В):
(45 - 15√15) / 10 = V (П) + 9
V (П) = (45 - 15√15) / 10 - 9
Отже, ми знайшли два можливих наближених значення швидкостей велосипедиста і пішохода, а саме:
1. V (В) ≈ 6,23 км/год і V (П) ≈ -2,57 км/год (заокруглені значення).
2. V (В) ≈ -2,57 км/год і V (П) ≈ 6,23 км/год (заокруглені значення).
Обидва варіанти мають сенс, але варіант, де швидкість велосипедиста додатня і більша за швидкість пішохода, є більш логічним. Таким чином, наші остаточні значення швидкостей:
Швидкість велосипедиста (V (В)) ≈ 6,23 км/год
Швидкість пішохода (V (П)) ≈ -2,57 км/год
Зауважте, що швидкість пішохода має негативний знак, що вказує на те, що пішохід рухався в протилежному напрямку до велосипедиста.
Объяснение: