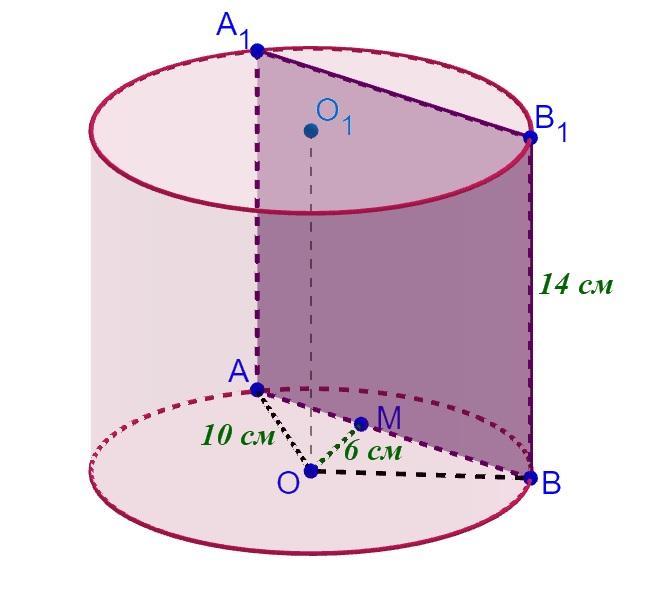
Висота ціліндра 14 см, радіус основи 10 см. Обчисліть площу перерізу , проведеного паралельно осі циліндра на відстані 6 см від неї.
Ответы
Ответ:
Площа перерізу дорівнює 224 см²
Объяснение:
Висота ціліндра 14 см, радіус основи 10 см. Обчисліть площу перерізу , проведеного паралельно осі циліндра на відстані 6 см від неї.
Маємо циліндр з радіусом R=OA=OB=10 см і висотою H=AA₁=BB₁=14 см, де AA₁B₁B – це переріз циліндра площиною, що проведений паралельно до його осі OO₁ на відстані 6 см.
Оскільки переріз AA₁B₁B паралельний до осі циліндра, то AA₁B₁B перпендикулярний до площини основи циліндра, тому AA₁B₁B – прямокутник з площею:
Sper = AB • AA₁ = AB • H.
З центра основи циліндра (кола) проведемо перпендикуляр OM=6 см до площини перерізу AA₁B₁B – відстань від осі циліндра до перерізу AA₁B₁B. Оскільки переріз перпендикулярний до площини основи циліндра, то OM⊥AB.
Розглянемо ΔAOB, у якого OA=OB=R=10 см як радіуси основи і OM=6 см – висота, що проведена до сторони AB.
Звідси слідує, що ΔAOB – рівнобедрений з основою AB, а OM – медіана і бісектриса, проведені до основи AB, тобто маємо:
AB = 2 · AM.
Із прямокутного ΔAOM (∠AMO=90°) за теоремою Піфагора знайдемо катет AM (OA=10 см – гіпотенуза, OM=6 см – катет):
АМ² = ОА² - ОМ² = 10² - 6² = 100 - 36 = 64
АМ = 8 (см)
Тоді:
АВ = 2 · 8 = 16 (см)
Площа перерізу (прямокутника AA₁B₁B):
Sper = AB • H = 16 · 14 = 224 (см²)
#SPJ1