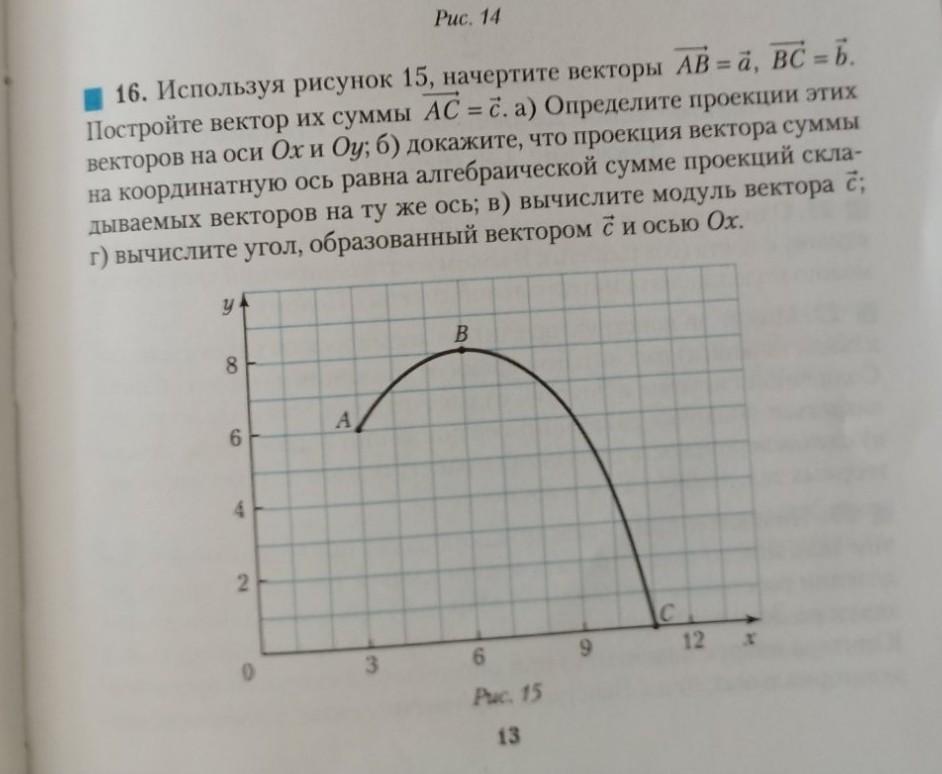
Используя рисунок 15, начертите векторы АВ→ = а→, ВС→ - b→. Постройте вектор их суммы АС = с→ а) Определите проекции этих векторов на оси Ох и Оу, б) докажите, что проекция вектора суммы на координатную ось равна алгебраической сумме проекций складываемых векторов на ту же ось; в) вычислите модуль вектора 2 г) вычислите угол, образованный вектором с→ и осью Ох
Ответы
На жаль, я не маю можливості відображати рисунки або малюнки. Проте, я можу надати інструкції для вирішення цього завдання з векторами.
Начертайте вектори A→ і B→: Відобразіть на площині два вектори A→ і B→, які представлені на рисунку 15. Для цього вказуйте напрямок і величину кожного вектора.
Знайдіть вектор с→ (сумма A→ і B→): Для цього просто додайте вектори A→ і B→ за законом паралельного переносу.
Знайдіть проекції векторів на осі Ох і Оу:
Проекція вектора A→ на ось Ох (Aₓ) - це x-компонента вектора A→.
Проекція вектора A→ на ось Оу (Aу) - це y-компонента вектора A→.
Аналогічно, знайдіть проекції вектора B→ на ось Ох (Bₓ) і Оу (Bу).
Доведіть, що справедлива рівність проекцій: Покажіть, що Aₓ + Bₓ = Cₓ і Aу + Bу = Cу. Це доведе рівність проекцій вектора с→ на координатні осі.
Знайдіть модуль вектора C→: Використовуючи теорему Піфагора, знайдіть модуль вектора C→: |C→| = √(Cₓ² + Cу²).
Знайдіть кут між вектором с→ і осью Ох: Використовуючи тригонометричні функції, обчисліть кут між вектором с→ і осью Ох: tan(θ) = (Cу / Cₓ), де θ - шуканий кут.
Це дозволить вам вирішити завдання, використовуючи дані про вектори A→ і B→ та їх суму C→.