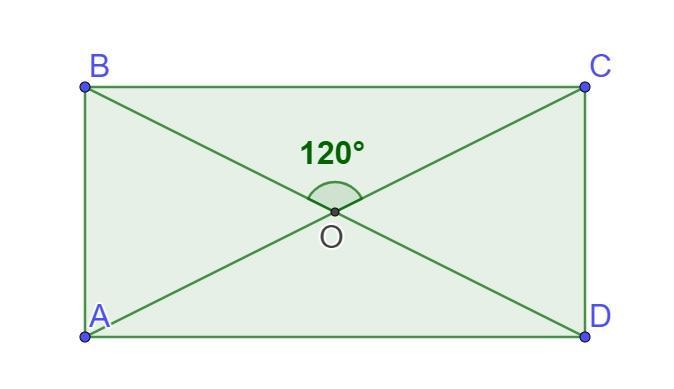
Тупий кут між діагоналями прямокутника дорівнює 120°. Доведи, що його діагональ у два рази більша за меншу сторону.
Ответы
Ответ:
Довели, що якщо тупий кут між діагоналями прямокутника дорівнює 120°, то діагональ прямокутника у два рази більша за меншу сторону.
Объяснение:
Тупий кут між діагоналями прямокутника дорівнює 120°. Доведи, що його діагональ у два рази більша за меншу сторону.
- Діагоналі прямокутника рівні.
- Діагоналі прямокутника перетинаються і точкою перетину діляться навпіл.
- В прямокутному трикутнику катет, що лежить проти кута 30 градусів дорівнює половині гіпотенузи
Дано: АВСD - прямокутник, АС∩ВD=О, ∠ВОС=120°
Довести: діагональ АС у два рази більша за сторону АВ.
Доведення
1) Розглянемо ΔВОС
ВО=ОС - за властивістю діагоналей прямокутника, отже ΔВОС - рівнобедрений з основою ВС.
∠ОВС=∠ОСВ - як кути при основі рівнобедреного трикутника.
Тоді за теоремою про суму кутів трикутника маємо:
∠ОВС=∠ОСВ=(180°-∠ВОС) : 2=(180°-120°) : 2 = 30°
2) Розглянемо прямокутний ΔАВС (∠АВС=90°)
∠АСВ=30°, АВ - катет, що лежить навпроти кута 30°, тому він дорівнює половині гіпотенузи АС:
АВ = 1/2 · АС
Тоді АС = 2 · АВ, що и треба було довести.
#SPJ1