5. При діленні двох двоцифрових чисел у частці отрима- ли 9, а в остачі 8. Чому дорівнює ділене?
Ответы
Ответ: 98, 107, 116, 125
Пошаговое объяснение:
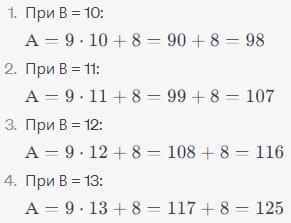
Щоб знайти ділене, ми можемо скористатися алгоритмом ділення. За умовою задачі, у частці отримали 9, а в остачі залишилося 8. Це означає, що ми можемо записати рівняння:
ділене = дільник * частка + остача
Позначимо ділене як "х", дільник як "у", частку як "ч" і остачу як "р". Тоді ми можемо записати рівняння наступним чином:
х = у * ч + р
За умовою задачі, частка (ч) дорівнює 9 і остача (р) дорівнює 8. Підставляючи ці значення в рівняння, отримуємо:
х = у * 9 + 8
Тепер нам потрібно знайти значення діленого (х). Для цього нам потрібно знайти значення дільника (у). Ми можемо перетворити рівняння, щоб виділити "у":
х - 8 = у * 9
Далі, ми можемо поділити обидві частини рівняння на 9:
(х - 8) / 9 = у
Тепер ми можемо підставити значення діленого (х) в це рівняння і обчислити значення дільника (у). Оскільки у нас немає конкретного числа для діленого, ми не можемо точно визначити значення дільника. Але ми можемо записати загальний вираз для дільника:
дільник = (ділене - остача) / частка
Таким чином, загальний вираз для дільника буде:
дільник = (х - 8) / 9
Отже, щоб знайти значення діленого, нам потрібно знати конкретне значення дільника.