Предмет: Геометрия,
автор: terzana981
Дано:
ABCD-четырёхугольник
AC-диагональ
Угол ABC=110°
Угол BCA=40°
BC||AD
Найти:
Угол CAD-?
Угол BAC-?
Приложения:
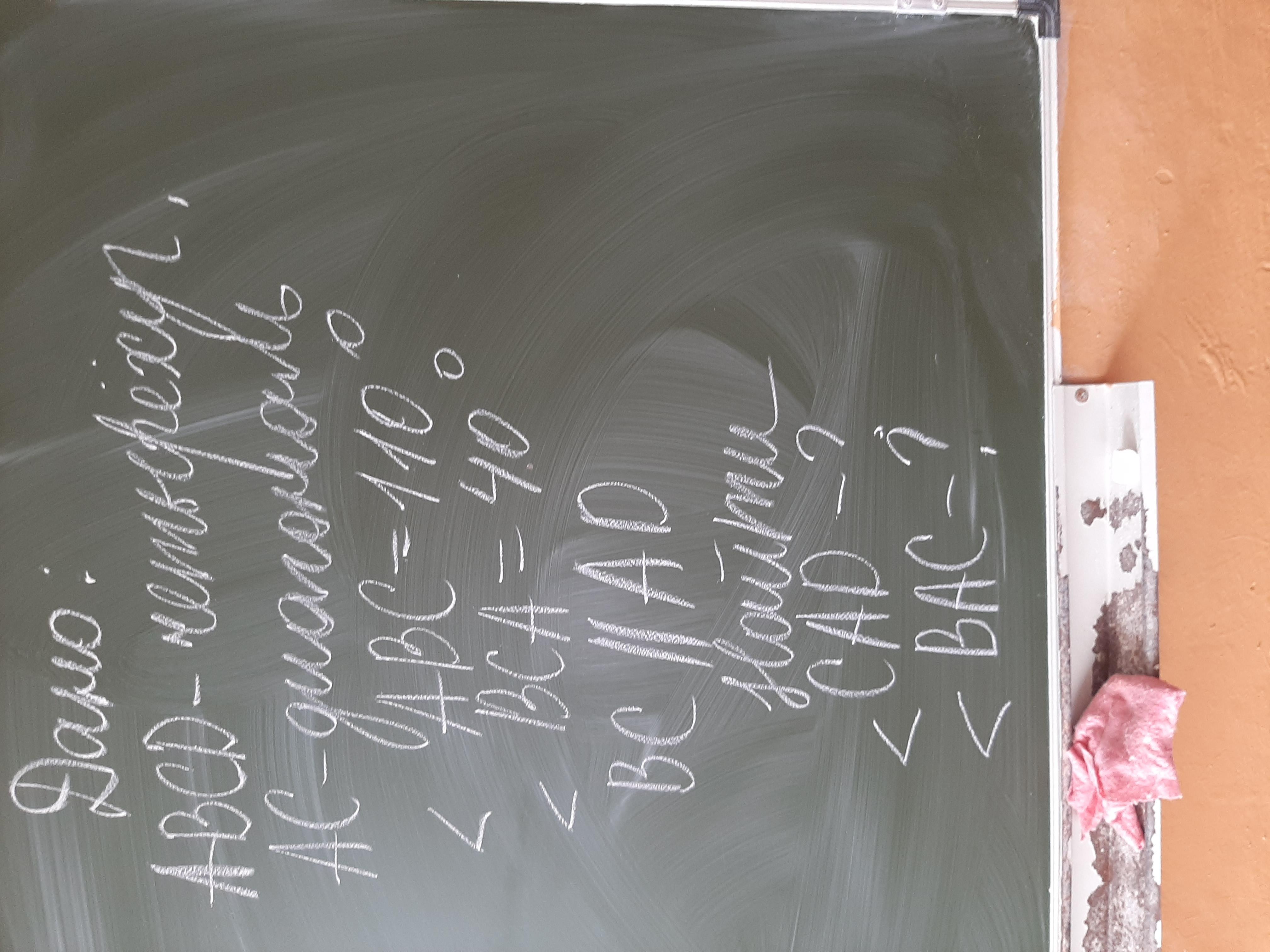
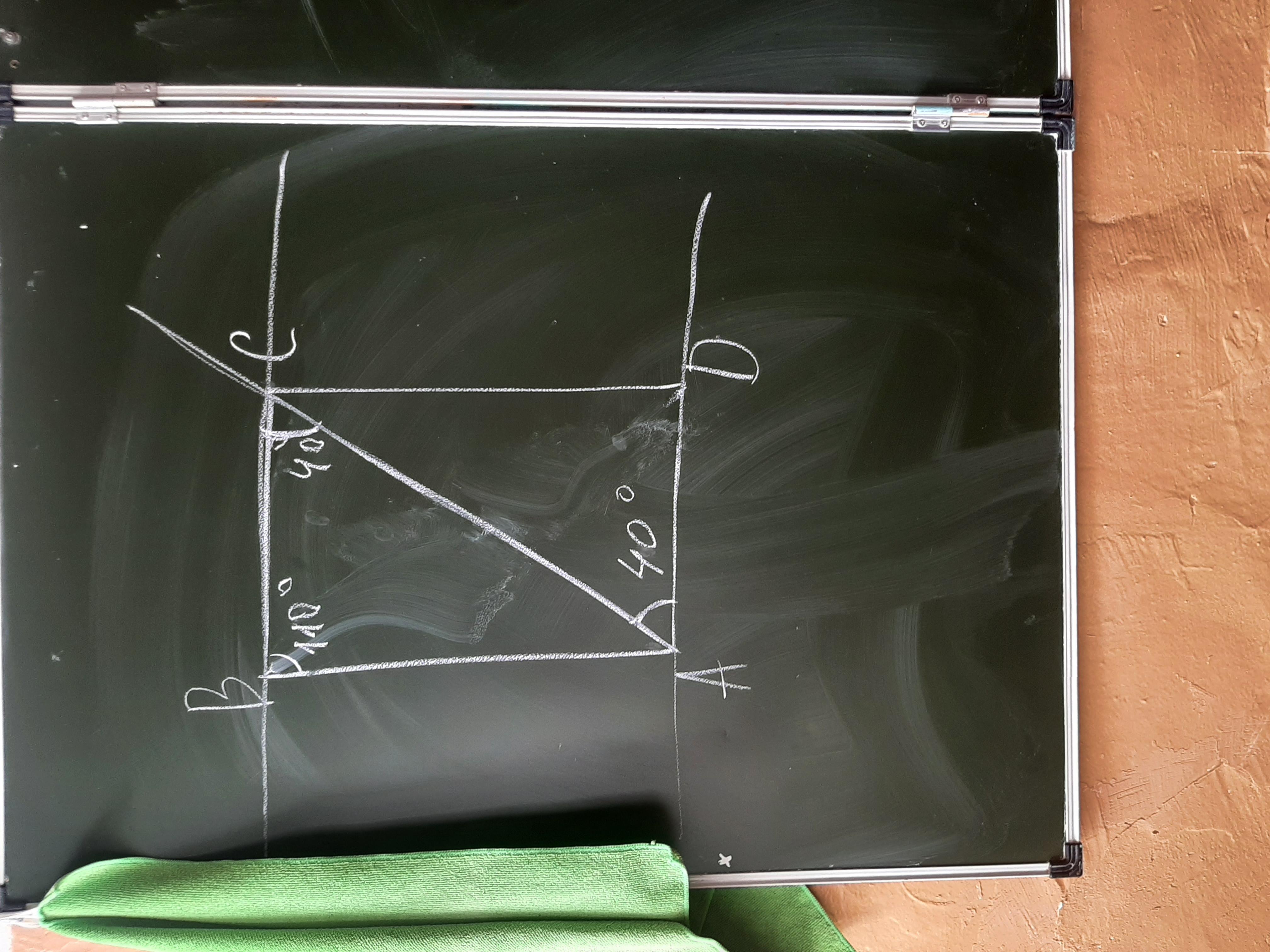
terzana981:
Помоги пожалуйста решить,срочно нужно
Ответы
Автор ответа:
0
Ответ:
BAC=30°
CAD=30°
Объяснение:
ezezez
Автор ответа:
0
Ответ:
Объяснение:
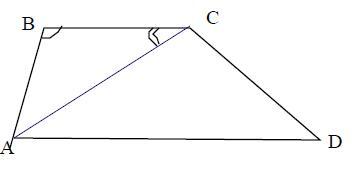
1. Т.к. ВС║AD по условию, а АВ∦ CD, то ABCD - трапеция.
2. ∠ВСА и ∠CAD - углы накрест лежащие при параллельных прямых ВС и AD и секущей АС. Следовательно, они равны.
∠ВСА = ∠CAD = 40°
3. Сумма углов трапеции, прилежащих к одной боковой стороне равна 180°. Значит,
∠В + ∠А = 180° или
∠В + (∠ВАС + ∠САD) = 180°
110° + ∠ВАС + 40° = 180°
∠ВАС + 150° = 180°
∠ВАС = 180°-150°
∠ВАС = 30°
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: adilhanmambetalievv
Предмет: История,
автор: davidlozovskij7
Предмет: Биология,
автор: bracilovitaha22
Предмет: Литература,
автор: ivantim41
Предмет: Русский язык,
автор: elgin219