Предмет: Алгебра,
автор: worldoftanksdanilgro
помогите пж ааааааааааааааааа
Приложения:
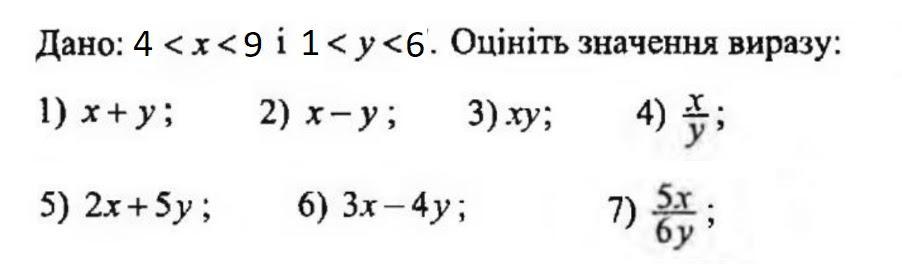
Ответы
Автор ответа:
2
Ответ:
1) 5 < x + y < 15
2) -2 < x - y < 8
3) 4 < xy < 54
4) 2/3 < xy < 9
5) 13 < 3x + 5y < 48
6) -12 < 3x - 4y < 23
7) 5/9 < 5x/6y < 15/2
Объяснение:
Дано: 4 < x < 9 и 1 < y < 6
Оценить значения выражений:
1) х + у
- Если неравенства одного знака сложить почленно, то получим верное неравенство.
2) x - y
- Если обе части неравенства умножить или разделить на отрицательное число, то знак неравенства перевернется.
1 < y < 6 | · (-1)
-1 > -y > -6 или -6 < -y < -1
Теперь можем сложить неравенства:
3) xy
- Если неравенства одного знака перемножить почленно, то получим верное неравенство.
4) х/у
- Если a < b и а > 0; b > 0, то 1/а > 1/b.
1 < y < 6
или
Перемножим:
5) 2x + 5y
- Если обе части неравенства умножить или разделить на положительное число, то получим верное неравенство.
4 < x < 9 |·2
8 < 2x < 18
1 < y < 6 |·5
5 < 5y < 30
Теперь сложим:
6) 3x - 4y
4 < x < 9 |·3
12 < 3x < 27
1 < y < 6 |·(-4)
-4 > -4y > -24 или -24 < -4y < -4
Теперь сложим:
7) 5x/6y
4 < x < 9 |·5
20 < 5x < 45
1 < y < 6
Можем перемножим:
#SPJ1
Похожие вопросы
Предмет: Алгебра,
автор: m76306217
Предмет: Математика,
автор: yanchuk2902
Предмет: История,
автор: Аноним
Предмет: Русский язык,
автор: ighjnbhej